|
|
|
How Does Tamiflu Work?
|
|
|
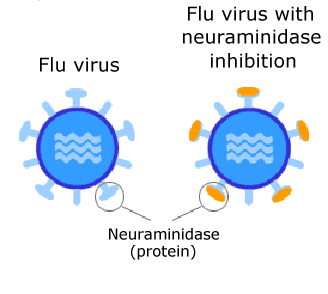
The neuraminidase coating on the influenza virus surface enables the
virus to chemically dissolve a pathway through the cell membranes of the human
body cells. By doing so it effectively invades the cells. Once in the cell it
replicates to form many new virus molecules. The new viruses leave the cell,
using the neuraminidase to break through the cell membrane, and invade adjoining
cells in the same way. The membrane of the cell they have left behind is broken
and as a result the cell itself dies. This process is repeated and an
efficient chain reaction is set up.
|
 |
|
Tamiflu
Hoffman La Roche
|
|
Once a number of cells have been affected, the patient would begin to
experience flu symptoms such as headaches and fevers etc. Tamiflu binds to
the neuraminidase on the surface of the virus particles and hence inhibits
the new viral particles' chemical ability to escape from the infected cell.
Hence the influenza virus is restricted to a smaller number of cells and the
body's immune system has a better chance of killing the virus.
Tamiflu is only able to inhibit the virus. There comes a point when the
number of infected cells is too large for the tamiflu to work effectively
therefore it must be taken as early as possible
|
BACK TO TOP
|
|
|