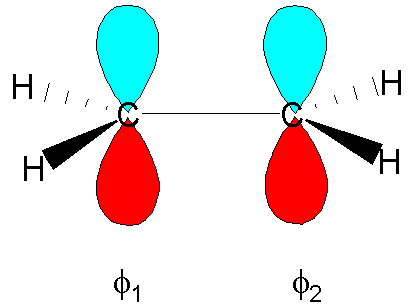
Finding the p molecular orbitals of ethane using the LCAO approximation

The expression for the energy can be written as:

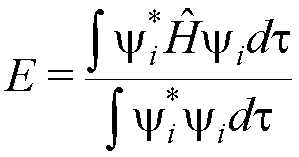
(this is the energy according to quantum mechanics: this energy is the ‘expectation value’ of the energy operator (Hamiltonian operator) for any wavefunction; in this case y_i is a molecular orbital of ethene).

The integrals are over all space. The energy calculated in this manner will depend on the coefficients c_i1, and c_i2

The variational principle states that if an approximate wavefunction (such as this) is used to calculate the energy, the value obtained for the energy is always greater than or equal to the exact ground state energy of the system, i.e.

E ³ E_exact

The Variation Principle (Atkins 7^th ed. pg. 429)

(This was covered in Prof. Balint-Kurti’s lectures on Quantum Concepts)

If an arbitrary or approximate wavefunction is used to calculate the energy of a system then the value obtained is always greater than or equal to the exact ground state energy of the system.

This principle can be stated mathematically as:

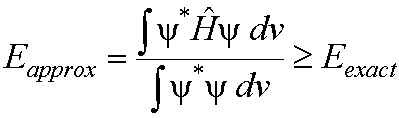(1)

Another way of saying this is

The energy of an approximate wavefunction is never less than the true energy

The Variation principle is the key to finding wavefunctions of molecules.

It leads to the Variational Method:

The Variational Method:

This is a method, based on the variational principle, for finding approximate wavefunctions.

It is central for finding electronic wavefunctions for molecules and enables us to calculate molecular orbitals, molecular electronic wavefunctions and potential energy curves and surfaces.

The method works as follows:

1. Construct an approximate wavefunction y which depends on some parameters c_i.

2. Calculate the energy using equation (1). The energy calculated in this way, E(c_i), will depend on the parameters c_i which are part of the approximate wavefunction.

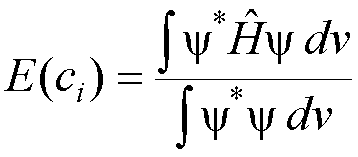(2)

3. Choose the parameters c_i so as to minimize the energy

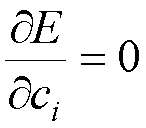(3)

· This minimized energy is still above the true ground state energy.

· The wavefunction with this set of parameters is the best wavefunction of the form which has been chosen.

· It gives the lowest possible energy, as close as possible to that of the exact ground state wavefunction.

So, for the p MOs of ethene:

· The next stage in this case is to minimize the energy with respect to the c_ip,, i.e, c_i1 and c_i2.

· This minimized energy will still be above the true ground state energy.

· The wavefunction with the values of c_i1 and c_i2 that give the minimum energy is the best wavefunction it is possible to obtain using just a simple combination of two atomic orbitals.

· It gives the energy closest to the exact ground state energy.

As you have seen in Prof. Balint-Kurti’s lectures this leads to secular equations:

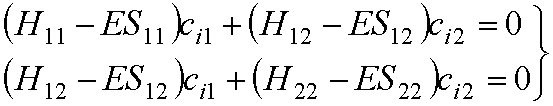
We can write them in matrix form:

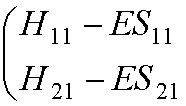
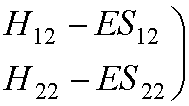
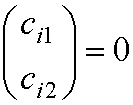
This leads to the secular determinant

The ‘trivial’ solution of these secular equations is

c_i1 = c_i2 = 0.

(Why is this of no interest?)

Next: the secular determinant and the energies of the molecular orbitals of ethene