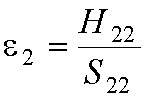A ‘nontrivial’ solution exists only if

det(H - ES) = 0,

i.e. if the determinant

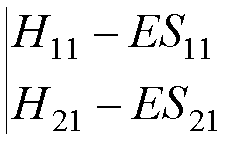
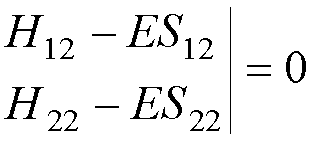
This determinant is known as the SECULAR DETERMINANT.

The equations use shorthand for the Hamiltonian integrals (‘matrix elements’), i.e. energies:

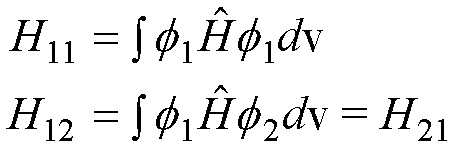
and the overlap integrals/matrix elements (the overlap is a number between 0 and 1):

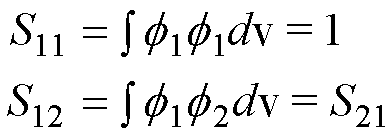
Note the symmetry H₁₂= H₂₁and S₁₂= S₂₁ in these matrix elements.

Expanding the secular determinant, we get a quadratic equation for E:

(H₁₁ - ES₁₁)(H₂₂ - ES₂₂) - (H₁₂ - ES₁₂)² = 0

· This means that there will be two values of E which satisfy this equation.

· These two values are the energies of the two molecular orbitals and the index “i” has been used to label them.

· We denote the two molecular orbital energies as E₁ and E₂.

· In our example, one will be the bonding, the other the antibonding p-orbital formed by the combination of the two C 2p orbitals.

The original atomic orbital energies, e₁ and e₂, are:

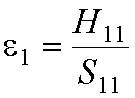and

The MOs must be normalized...