Chapter 5

 

Electrochemical studies of moderately boron doped diamond in non aqueous electrolyte

 

5.1. Introduction

 

Studies of diamond electrodes in non aqueous solvents are very limited. It has been reported that diamond electrodes in non aqueous electrolyte posses an increased potential, allowing a fifth peak for the reduction of C₆₀ to be observed ¹. In addition diamond electrodes have been employed in the generation of solvated electrons in ammonia ². Both studies were performed using highly boron doped diamond. In this chapter, electrochemical studies of moderately boron doped diamond in non-aqueous solvents are presented. A proper investigation requires locating the band edges in the chosen medium. The determination of the band edges is performed by Mott-Shottky studies. These allow the calculation of the flat band potential and therefore the band edges. As diamond electrodes are under influence of their surface termination separate Mott-Shottky studies are required with hydrogen and oxygen terminated diamond electrodes. Additional cyclic voltammetric studies are presented for both types of surface termination.       Mott-Shottky data and cyclic voltammograms are compared and explained in terms of the band edge localisation and the theory developed in the chapter 4.

 

5.2. Potential distribution across the semiconductor-electrolyte interface

 

Consider initially a p-type semiconductor in equilibrium with a redox couple. Equilibrium is reached when the Fermi level of the semiconductor is equal to the Fermi energy associated with the redox couple (see figure 5.1)

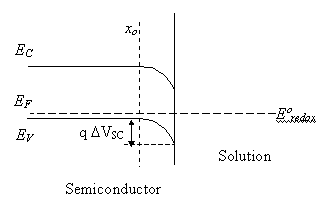
Figure 5.1. Energy diagram of the semiconductor-electrolyte interface under equilibrium. The Fermi level energy (E_F) is equal to the redox potential energy (Eº_redox).

 

The depletion layer, more commonly known as space charge region, produces a bending of the bands to lower energies.

 

Under potentiostatic control the applied potential is established between the working electrode and the reference electrode. If the interface is considered as ideally polarizable (electrons cannot be exchanged with the electrolyte), the zero of potential is that at which the potential in the bulk semiconductor matches that of redox couple ate the reference electrode, see figure 5.2.

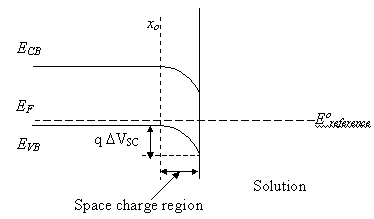
Figure 5.2. Energy diagram of an ideally polarisable interface at zero potential. The Fermi level energy (E_F) is equal to the reference electrode energy (Eº_reference).

 

From figure 5.2 it is apparent that the concentration of the electrons in the space charge region depends on the potential difference between the working electrode (semiconductor) and the reference. At this point it is necessary to consider the other side of the working electrode/ electrolyte junction, the Helmholtz double layer. Briefly, when the supporting electrolyte is in high concentration, this region contains the nonadsorbed ions that represent the counter charge. The thickness of this layer is smaller than the space charge region (see figure 5.3).

Figure 5.3. Schematic representation of the potential drop (a) and charge across the semiconductor electrolyte interface under depletion conditions.

 

In figure 5.3.a the potential distribution across the interface is shown taking the potential of the bulk of the solution as zero. The potential drop across the space charge region (DV_SC) occurs over a larger distance than the potential drop across the Helmholtz layer (DV_H), this is because DV_SC results from ionisation of the acceptors in the solid, whilst DV_H is due to the ions accumulated a few angstroms away from the surface (see figure 5.3b).

 

Since the charge in both regions is equal but with opposite sign, the capacitance of the space charge region is normally negligible in comparison to the Helmholtz capacitance. Under these conditions, DV_H is constant and any possible change in the applied potential between working and reference electrode will appear in DV_SC. Thus the potential in the bulk of the working electrodes (E) is given by:

 

                                                                                                             [equation 5.1]

 

 where V_fb is the flat band potential. At this potential, the surface concentration of holes is equal to the bulk. At more positive potentials than the V_fb, the surface concentration of electrons is decreased creating an accumulation layer of majority carriers and the bending of the bands at the surface to higher energies. At potentials more negative than the V_fb, electrons produce a depletion layer, bending downwards at the surface to lower energies (see figure 5.4).

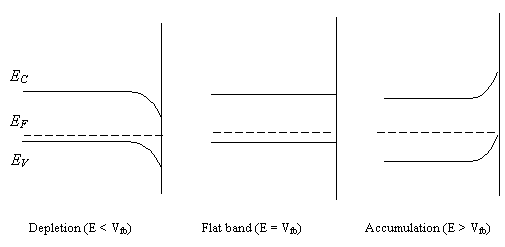
Figure 5.4. Potential dependence of the band bending for a p-type semiconductor.  N_SC : free carrier concentration

 

Under depletion conditions, charging comes from the electron affinity of the acceptors. If the density of the charge is assumed constant in the space charge region, Poisson’s equation can be written as

 

                                                                                                             [equation 5.2]

 

After integrating twice and assuming that the electric field (dV/dx) is zero at x_o, a long way from the surface and that V is zero in the bulk of the semiconductor, the Shottky relation can be obtained

 

                                                                                                            [equation 5.3]

 

where w is the width of the space charge region.

 

Considering Gauss’s law:

 

                                                                                                            [equation 5.4]

 

where A is the surface area of the electrode. Substituting the integrated Poisson’s equation into equation 5.4, the capacitance of the space charge region (C_SC) is

 

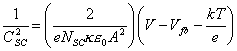
                                                                                                            [equation 5.5]

 

The above equation is known as Mott-Schottky relationship. From equation 5.5, C_SC^-2 is linearly dependent on V, with the slope inversely proportional to N_SC and  related  to V_fb.

 

The flatband potential is important in determining the conduction or the valence band edges for a semiconductor on the vacuum reference scale of energies. Once V_fb is known, E_VB and E_CB can be calculated from the relations

 

           

                                                (p-type semiconductor)             [equation 5.6]

 

 

                                                                (n-type semiconductor)             [equation 5.7]

 

 

where E_VB and E_CB are the band edges of the valence band and the conduction band; N_VB and N_CB, are the effective density of states in the valence and conduction bands respectively for a p- and n-type semiconductors, data obtained from solid state measurements. Once E_CB or E_VB is determined the other can be easily found provided E_g is known.

 

 5.3. Experimental set-up

 

Electrochemical experiments were performed using a three electrode system. This section descibes the apparatus used.

 

5.3.1. Electrolyte solutions

 

Anhydrous acetronitrile (99.9% pure) was used as solvent and 0.1 mol dm^-3 tetrabutylammonium perchorate (TBAP) as supporting electrolyte.

 

Two different solutions were prepared contaning 1´10^-3 mol dm^-3 of either ferrocene (FeCp₂) or bis(pentamethylcyclopentadienyl) iron (FeCp₂^*).

 

Glassware was cleaned with a five step process:

 

1.      soaking in a chromic acid bath (saturated potasium dichromate (K₂Cr₂O₇) in concentrated sulfuric acid (H₂SO₄).

2.      immersing and rinsing in deionised water (18.3 MW cm ultrapure deionised

water (Millipore)).

3.      soaking in an aqua regia bath (1:3 nitric acid (HNO₃)/ hydrochloric acid  (HCl)).

4.      inmmersing and rising in deionised water.

5.      placing in an oven at 100ºC for 30 minutes and checking no moisture remained.

 

After this routine all the glassware was kept in the dry box under argon atmosphere.

 

All the solutions were prepared under dry box conditions to ensure that no moisture or oxygen entered the solutions. To double check that no residual oxygen was present in the solutions they were purged with standard laboratoy grade oxygen-free argon (Ar) for aproximmately 10 minutes inside the dry box before any electrochemical experiment was done.

 

5.3.2    Electrochemical Cells

 

The main type of cell used in these studies was a single chamber design. A schematic diagram is shown in figure 5.5. This cell design proved ideal for performing electrochemistry with silver paint, three layer metal and titanium underlayer contacts.

 

The electrochemical cells were fabricated from white cylinders of PTFE † (50 mm in diameter). A central bore was removed from the main segment of the cell to provide a reservoir for the electrolyte. The diamond sample that was to be used as a working electrode (WE) was laid horizontally and sandwiched between two PTFE cylinders. A 4mm hole in the base of the main piece and an ‘O’ ring (3.5 mm internal diameter) exposed a selected area of the electrode surface to the electrolyte. Therefore, the approximate electrode area exposed to the electrolyte was 0.4 cm² (40 mm²).

Figure 5.5.  A schematic diagram of an electrochemistry cell

 

The base of the cell was tapered to allow small samples to be used. All samples had to be flat and the minimum sample size was 1 cm ´ 1 cm. Typical sample dimensions were 1.5 cm ´ 1 cm.

 

The bottom piece of PTFE was attached to a brass plate to provide a stable base.

 

A transparent top piece was fitted over the cell. The reference electrode (RE) and the counter electrode (CE) were placed through holes in the top. They were held in place by rubber rings (not illustrated in figure 5.5). Two additional holes allowed for deoxygenating to be performed. Argon could be bubbled through the electrolyte via a needle that was passed down into the solution.

 

Control experiments could be performed with platinum (Pt) working electrodes. Platinum wires could be passed down through one of the gas inlets.

 

5.3.3. Counter Electrodes

 

Platinum (Pt) counter electrodes were made from a curled square of platinum mesh attached to a platinum wire. This provided a suitably large surface area. A glass tube was used to hold the electrode. This was designed with the same diameter as the reference electrode. The tube was sealed to the platinum wire at the bottom of the electrode. The top of the tube, which was never submersed into the electrolyte, was sealed with epoxy resin. Nickel wire was used inside the glass tube because it was less expensive than the platinum wire. The wire was wound round a notch at the top of the electrode, so that the weight of the attached crocodile clip did not apply a force on to the platinum-nickel join or the platinum-glass seal. A quick fit stopper was fitted to the top of the electrode to provide compatability with a number of other designs of electrochemical cell. A diagram of a counter electrode is shown in figure 5.6.

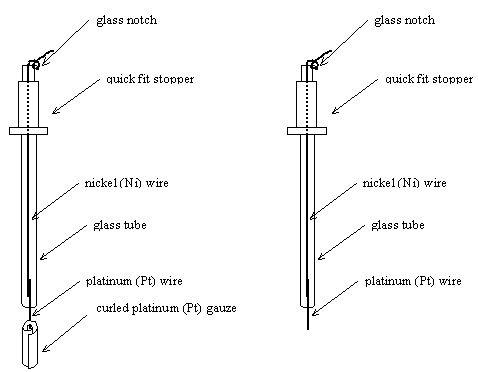
Figure 5.6. In the left side, a schematic diagram of a platinum counter electrode. In the right side, a schematic diagram of a platinum wire electrode.

 

5.3.4. Reference Electrodes

 

Ferrocene | Ferrocenium cation (FeCp₂|FeCp₂⁺) reference electrodes were used. These electrodes were made from a glass frit and a platinum wire electrode. The glass frit was filled with a solution containing 1´10^-3 mol dm^-3 of ferrocene/ferrocenium in 0.1 mol dm^-3 of TBAP/CH₃CN (see figure 5.7). To avoid any possible evaporation process the top of the reference electrode (where the glass frit and the platinum counter electrode join) was sealed with PTFE tape.

 

The formal potentials, Eº¢, are given in this chapter vs ferrocene | ferrocenium couple, as recommended by IUPAC ³ when the electrolyte is not aqueous. The formal potential for FeCp₂ | FeCp₂⁺ is 0.38 V relative to the aqueous satured calomel electrode (SCE) at 298 K ⁴.

 

Experimental measurements were done to check the relationship of the ferrocene couple and SCE. Neglegible differences were observed between the experimental and the literature data.

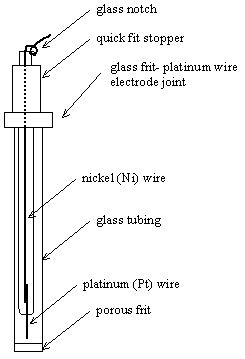
Figure 5.7. A schematic diagram of a ferrocene reference electrode.

 

5.3.5    Potentiostats

 

Cyclic voltammometric measurements were performed using an EG&G 273 Princeton Applied Research instrument that was controlled using Research Electrochemistry software.

 

Impedance measurements were performed using a Solartron 1286 potentiostat and a Solartron 1250 Frequency Response Analyser (FRA). The instruments were controlled using Z-plot software. In all ac experiments a modulation amplitude of 10 mV was applied.

 

5.3.6. The dry box      

 

A standard dry box was modified on one side to install one parallel and three BNC electrical connections. This modification allowed control of the electrochemical experiments through a computer. The dry box operates in a simple way. It is continuously filled by argon gas (standard laboratoy grade oxygen-free argon gas cylinder (BOC)). During that process as oxygen is lighter than argon oxygen will be removed through the exhaust lines. The argon gas is dried when it passes thorough a column filled with dry sieves. A pump is used to recirculate the argon gas. An air-lock is employed to allow materials to be put in and out material without introducing moisture or oxygen to the dry box. Neoprene gloves are used to operate inside the dry box (see figure 5.8).

 

Figure 5.8. A picture of the dry box

 

All electrochemical experiments were performed in the dry box in such conditions that the amount of water vapour was less than 6 ppm by volume.

 

5.4. Mott-Schottky Plots

 

To establish the position of the band edges of p-type diamond in acetonitrile Mott-Schottky analyses were undertaken.

 

Plots 1/(capacitance)² against applied potential, recorded at different frequencies, for both hydrogenated and oxygenated boron doped diamond electrodes immersed in acetronitrile containing  0.1 mol dm^-3 TBAP are displayed in figure 5.9 and figure 5.10.

Although Mott-Schottky theory suggests that plots should be independent of the measuring frequency (see section 5.2) this behaviour is rarely observed for semiconductor electrodes.

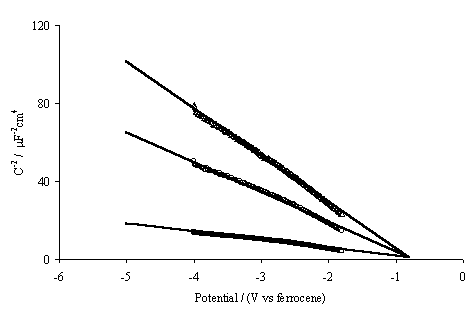
Figure 5.9. Mott-Schottky plots for semiconducting hydrogen terminated boron doped diamond electrode. Three frequencies of modulation were recorded; D 10 KHz, O 5 KHz and ÿ 1 KHz. Linear extrapolation of the experimental data has a common intercept approximately –0.8 V. Potential relative to the ferrocene standard couple.

 

Figure 5.10. Mott-Schottky plots for semiconducting oxygen terminated boron doped diamond electrode. Three frequencies of modulation were recorded; à 20 KHz, O 10 KHz and [] 5 KHz. Linear extrapolation of the experimental data has a common intercept approximately 1.5 V. Potential relative to the ferrocene standard couple.

 

Surface roughness, dielectric relaxation and the influence of surface states have been advanced as explanations of the frequency dispersion in Mott-Schottky plots⁵.

 

In order to calculate the free carrier concentration equation 5.5 at 298 K (N_SC in cm^-3,V  in  V, C_SC in mFcm^-2) can be simplified to:

 

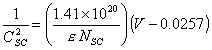
                                                                                                [equation 5.8]

 

where diamond e = 5.5.

 

Using the data recorded at a frequency of 10 KHz a free carrier concentration (N_SC) of 1.1´10¹⁸ cm^-3    was determined for both the hydrogenated and oxygenated samples. This figure compares favourably with the experimental conditions employed during film preparation; a boron to carbon ratio of 50 ppm in the gas phase suggest a boron density of 5.7´10¹⁸ cm^-3 in the crystal, assuming the boron concentration in the solid is directly proportional to that in the gas phase.

 

At the hydrogenated surface the Mott-Schottky plots are linear between –1.8 V and –4.0 V and posses a common intercept. The plots indicate that the valence band edge (using equation 5.6), relative to the ferrocene couple, lies at –0.8V. Given that the bandgap of diamond is 5.4 eV this places the conduction band edge at –6.2 V on the same scale, or at +1.3 eV relative to an electron in a vacuum ⁶. The fact that hydrogen terminated diamond has negative electron affinity is one of the key reasons why this material is being considered in field emission devices ^7-23.

 

The change in surface bond polarisation at the oxygen terminated surface relative to the hydrogenated surface results in a large shift in the band edges ²⁴. This is evident in the Mott-Schottky data for the oxygenated p-type diamond electrode. In the case of the oxygenated diamond surface a linear region is observed between 0.3V and –2.0 V; as for the hydrogen terminated surface frequency dispersion is evident but a common intercept is attained.

 

Analysis of the data indicates that for oxygen terminated p-type diamond electrode in acetonitrile the valence band edge lies at 1.5 V and the conduction band edge at –3.9 V ²⁵, indicating positive electron affinity.

 

In figure 5.7 the energy levels for the oxygen and hydrogen terminated surfaces of p-type diamond, as determined from Mott-Schottky data, are shown. In addition the energy levels of some common non-aqueous outer sphere redox couples are displayed ^{4, 26}. To facilitate discussion the electron affinity of graphitic carbon is also plotted, this energy level is a guide to energy of graphitic surface states at the diamond/electrolyte interface ⁶. Elemental boron surface states are approximately placed in the energy diagram ^{27, 28}.

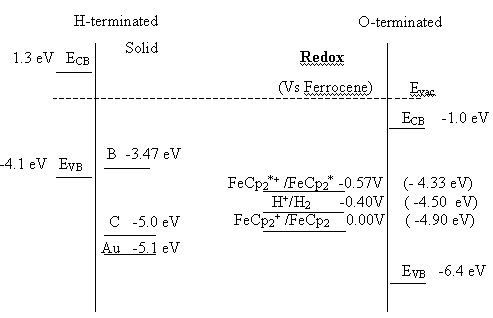
Figure 5.11. Proposed energy diagram for the diamond-electrolyte interface for hydrogen and oxygen terminated samples.  H+/H₂ = -0.4 V, FeCp₂⁺ /FeCp₂    0.00V     ( -4.90 eV)

 

5.5. Cyclic voltammograms

 

In the figures 5.12 and 5.13 cyclic voltammograms for a platinum working electrode in 1´10^-3 mol dm^-3 FeCp₂ and 1´10^-3 mol dm^-3 FeCp₂^* in 0.1 M TBAP/MeCN respectively are displayed.

 

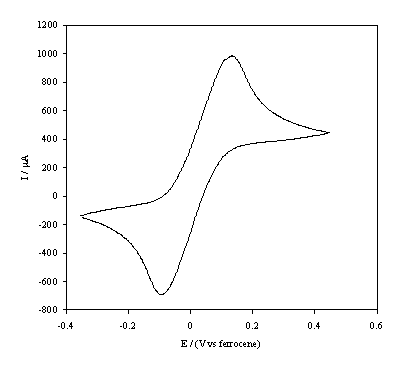
Figure 5.12. Cyclic voltammetric i-E curve recorded at a scan rate of 0.1 V s^-1, of platinum working electrode in  1´10^-3 mol dm^-3 FeCp₂.

 

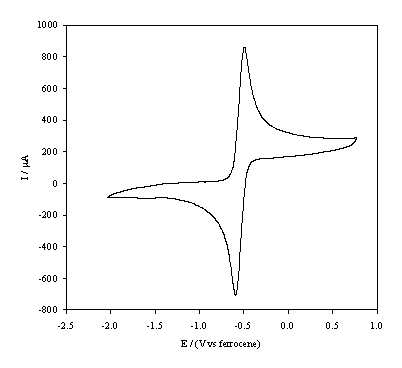
Figure 5.13. Cyclic voltammetric i-E curve recorded at a scan rate of 0.1 V s^-1, of platinum working electrode in  1´10^-3 mol dm^-3 FeCp₂^*.

 

In the figures 5.14, 5.15, 5.16, 5.17 cyclic voltammograms for hydrogen and oxygen surface terminated diamond in both 1´10^-3 mol dm^-3 FeCp₂ and 1´10^-3 mol dm^-3 FeCp₂^* in 0.1 M TBAP/MeCN are displayed.

 

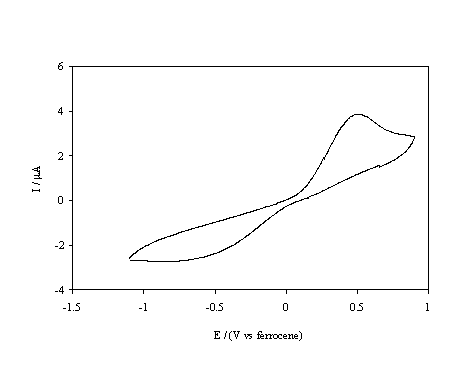
Figure 5.14. Cyclic voltammetric i-E curve recorded at a scan rate of 0.1 V s^-1, of boron doped diamond electrode. A hydrogen terminated sample immersed in  1´10^-3 mol dm^-3 FeCp₂.

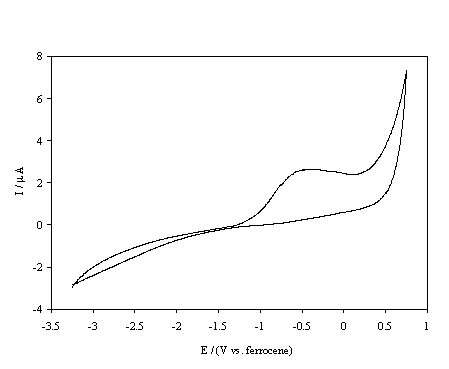
Figure 5.15. Cyclic voltammetric i-E curve recorded at a scan rate of 0.1 V s^-1, of boron doped diamond electrode. A hydrogen terminated sample immersed in 1´10^-3 mol dm^-3 FeCp₂^*.

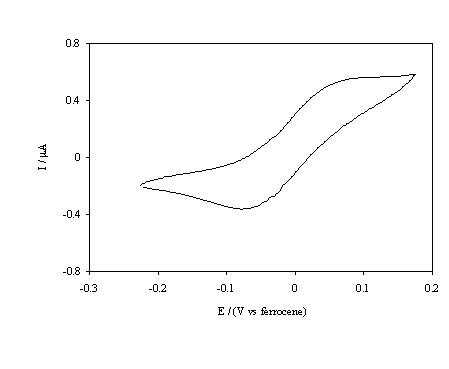
Figure 5.16. Cyclic voltammetric i-E curve recorded at a scan rate of 0.1 V s^-1, of boron doped diamond electrode. An oxygen terminated sample immersed in 1´10^-3 mol dm^-3 FeCp₂.

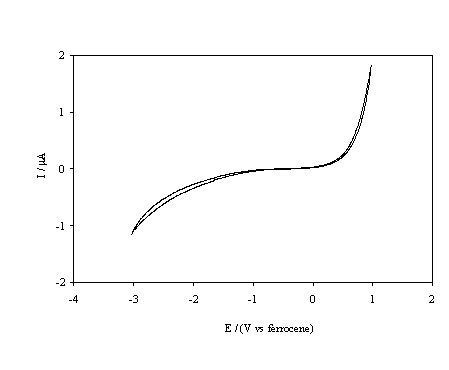
Figure 5.17. Cyclic voltammetric i-E curve recorded at a scan rate of 0.1 V s^-1, of boron doped diamond electrode. An oxygen terminated sample immersed in  1´10^-3 mol dm^-3 FeCp₂^*.

 

At the hydrogen terminated surface, figure 5.14, well defined oxidation and reduction peaks are observed for the FeCp₂⁺ / FeCp₂ redox couple. The cathodic peak is distorted and the peak separation is approximately 1.2 V; it should be noted that the material was highly resistive and no iR compensation was employed when recording the voltammograms, and the kinetics of the redox couple appears to be slow. In contrast figure 5.15 shows that the oxidation of FeCp₂^* at the same surface is irreversible with negligible cathodic currents until voltages less than ‑2.5 V are achieved. This behaviour is explained in terms of the classical Marcus-Gerischer mechanism of electron transfer ^{6, 29-31}. Reference to figure 5.11 indicates that the redox level of the FeCp₂⁺ / FeCp₂ couple lies within the valence band of the hydrogen terminated p-type diamond. Hence at the redox potential of the couple the Fermi level lies within a semiconductor band and reversible electrochemistry is observed. In comparison the redox level of the FeCp₂^*+ / FeCp₂^* couple lies almost at the band edge of the hydrogen terminated p-type diamond.  Therefore, an anodic current flows only at potentials under which holes accumulate at the electrode surface whilst a small constant cathodic current flows due to the negligible overlap between the energy levels of the oxidised states and the valence band edge. At high negative overpotentials an increased cathodic current may be observed due to breakdown of the Schottky barrier. In summary the results indicate that the hydrogen terminated material is acting as a p-type semiconductor electrode when used in non-aqueous solvents.

 

The large shift in the band edges with change in surface termination of p-type diamond results in the cyclic voltammograms recorded at the oxygen terminated surface being markedly different to those of the hydrogen terminated surface. The cyclic voltammogram in figure 5.16 indicates that for the FeCp₂⁺ / FeCp₂ couple anodic and cathodic currents are observed at the oxygenated surface. The current magnitude is considerably less than that for the hydrogenated surface despite identical experimental parameters. In figure 5.17 the cyclic voltammogram for the FeCp₂^*+ / FeCp₂^* couple is displayed, it is apparent that this couple is inactive within the potential window of the solvent. The energy levels that are shown in figure 5.11 indicate that both redox couples investigated are situated between the band edges of the oxygen terminated surface.

 

 The observation that FeCp₂^* is not oxidised indicates that in the potential range of interest the p-type oxygenated diamond surface is in depletion and not inversion. It is, therefore, difficult to justify the anodic peak observed in the FeCp₂ voltammogram simply in terms of direct charge transfer between the valence band of the material and the redox couple. In studies of oxygenated p-type diamond electrochemistry involving aqueous electrolytes evidence for surface state mediated charge transfer has been observed ^32-34. It has been suggested that the surface states involved in the charge transfer are graphitic in character. The results reported above support this proposal. Figure 5.11 indicates that the FeCp₂ couple is close in energy to graphitic states whilst the FeCp₂^* redox couple lies at greater energy than the surface states. This indicates that graphitic state mediated charge transfer will be facile for the FeCp₂ couple but difficult for the FeCp₂^* couple, as observed.

 

5.6. Conclusions

 

Studies of moderately boron doped diamond in non-aqueous solvents have permitted the influence of surface termination on the electrochemical behaviour of this semiconductor to be investigated. It was shown that the surface termination is important in two respects. First, it determines the position of the band edges. These may shift by approximately 2.3 V on going from an oxygen terminated to a hydrogen terminated surface. Second, graphitic surface states may mediate charge transfer. For the hydrogen terminated diamond surface the electrochemical studies in non-aqueous solvent showed characteristics of a non-degenerately doped p-type semiconducting material, to the authors' knowledge this is the first time such behaviour has been observed for a non-oxidised diamond electrode. For the oxygen terminated surface it was demonstrated that reversible cyclic voltammograms are only observed for redox couples of comparable energy to graphitic surface states.

 

5.7. References

 

¹              Z. Y. Wu, T. Yano, D. A. Tryk, K. Hashimoto, and A. Fujishima, Chem. Lett., 1998, 503.

²              F. J. Del Campo, C. H. Goeting, D. Morris, J. S. Foord, A. Neudeck, R. G. Compton, and F. Marken, Electrochem. and Solid State Lett., 2000, 3, 224.

³              G. Gritzner and J. Kuta, J. Pure Appl. Chem., 1984, 56, 461.

⁴              N. G. Connelly and W. E. Geiger, Chem. Rev., 1996, 96, 877.

⁵              W. P. Gomes and F. Cardon, Prog. Surf. Sci., 1982, 12, 155.

⁶              S. R. Morrison, 'Electrochemistry at Semiconductor  and Oxidized Metal Electrodes', Plenum Press, 1980.

⁷              Y. C. Yu, J. H. Huang, and I. N. Lin, J. Vac. Sci. Technol. B, 2001, 19, 975.

⁸              A. Fujishima and T. N. Rao, Diam. Relat. Mater., 2001, 10, 1799.

⁹              J. Ristein, Diam. Relat. Mater., 2000, 9, 1129.

¹⁰             N. Koenigsfeld, B. Philosoph, and R. Kalish, Diam. Relat. Mater., 2000, 9, 1218.

¹¹             J. B. Cui, J. Ristein, M. Stammler, K. Janischowsky, G. Kleber, and L. Ley, Diam. Relat. Mater., 2000, 9, 1143.

¹²             A. Wisitsora-at, W. P. Kang, J. L. Davidson, Y. Gurbuz, and D. V. Kerns, Diam. Relat. Mater., 1999, 8, 1220.

¹³             P. W. May, M. T. Kuo, and M. N. R. Ashfold, Diam. Relat. Mater., 1999, 8, 1490.

¹⁴             A. V. Karabutov, V. D. Frolov, S. M. Pimenov, and V. I. Konov, Diam. Relat. Mater., 1999, 8, 763.

¹⁵             T. Sugino, Y. Iwasaki, S. Kawasaki, Y. Yuuko, R. Hattori, and J. Shirafuji, Diam. Relat. Mater., 1998, 7, 677.

¹⁶             A. N. Obraztsov, I. Y. Pavlovsky, A. P. Volkov, E. V. Rakova, and S. P. Nagovitsyn, J. Electrochemical Soc., 1998, 145, 2572.

¹⁷             R. J. Nemanich, P. K. Baumann, M. C. Benjamin, O.-H. Nam, A. T. Sowers, B. L. Ward, H. A. de, and R.F.Davis, Appl. Surf. Sci., 1998, 130, 694.

¹⁸             P. W. May, J. C. Stone, M. N. R. Ashfold, K. R. Hallam, W. N. Wang, and N. A. Fox, Diam. Relat. Mater., 1998, 7, 671.

¹⁹             P. W. May, S. Hohn, W. N. Wang, and N. A. Fox, Appl. Phys. Lett., 1998, 72, 2182.

²⁰             P. W. May, S. Hohn, M. N. R. Ashfold, W. N. Wang, N. A. Fox, T. J. Davis, and J. W. Steeds, J.Appl. Phys., 1998, 84, 1618.

²¹             U. Hoffman, A. Weber, T. Lohken, C.-P. Klages, C. Spaeth, and F. Richter, Diam. Relat. Mater., 1998, 7, 682.

²²             M. W. Geis, N. N. Efremow, K. E. Krohn, J. C. Twichell, T. M. Lyszczarz, R. Kalish, J. A. Greer, and M.D.Tabat, Nature, 1998, 393, 431.

²³             B. L. Druz, V. I. Polyakov, A. V. Karabutov, N. M. Rossukanyi, A. I. Rukovishnicov, E. Ostan, A. Hayes, V. D. Frolov, and V. I. Konov, Diam. Relat. Mater., 1998, 7, 695.

²⁴             J. van de Lagemaat, D. Vanmaekelbergh, and J. J. Kelly, J. Electroanal. Chem., 1999, 475, 139.

²⁵             P. K. Baumann, S. P. Bozeman, B. L. Ward, and R. J. Nemanich, Diam. Relat. Mater., 1997, 6, 398.

²⁶             D. R. Lide, in 'CRC Handbook of Chemistry and Physics', ed. D. R. Lide, 1994.

²⁷             C. E. Nebel, E. Rohrer, and M. Stutzmann, J.Appl. Phys., 2001, 89, 2237.

²⁸             C. E. Nebel, M. Stutzmann, F. Lacher, P. Koidl, and R. Zachai, Diam. Relat. Mater., 1998, 7, 556.

²⁹             A. J. Bard and L. R. Faulkner, 'Electrochemical Methods Fundamentals and Applications', 2001.

³⁰             R. A. Marcus, J. Chem. Phys., 1965, 43, 679.

³¹             R. A. Marcus., J. Chem. Phys., 1956, 24, 966.

³²             S. Alehashem, F. Chambers, J. W. Strojek, G. M. Swain, and R. Ramesham, Anal. Chem., 1995, 67, 2812.

³³             D. Vanmaekelbergh, J. J. Kelly, S. Lingier, and W. P. Gomes, Ber. Bunsen-Ges. Phys. Chem. Chem. Phys., 1988, 92, 1068.

³⁴             M. N. Latto, D. J. Riley, and P. W. May, Diam. Relat. Mater., 2000, 9, 1181.