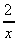 - 2 (b) 3 -
- 2 (b) 3 - 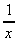 (c)
(c) 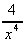 + 6 (d)
+ 6 (d) 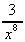 -
- 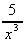
These are to be discussed in your tutorial in week 5.
1. Differentiate the following expressions:
(a) 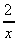 - 2 (b) 3 -
- 2 (b) 3 - 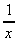 (c)
(c) 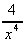 + 6 (d)
+ 6 (d) 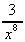 -
- 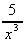
(e) 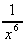 -
- 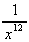 (the
Lennard-Jones potential) (f) 3
(the
Lennard-Jones potential) (f) 3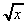
(g) 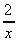 -
- 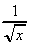 (h)
3
(h)
3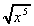 (i)
(i) 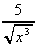 +
+ 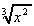 (j)
(j) 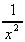 -
- 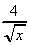 +
+  -
-
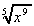
2. What is the value of the gradient of these functions when:
(a) y = 5x2 +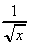 , when
x = 2 (b) p =
, when
x = 2 (b) p = 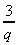 + 6 , when
q = 3
+ 6 , when
q = 3
(c) φ = x - ![]() , when x = 1.2 (d) Z = 3ζ2 + ζ½ - ζ7/3 , when ζ = 0.1
, when x = 1.2 (d) Z = 3ζ2 + ζ½ - ζ7/3 , when ζ = 0.1
3. Find the value(s) of x at which the following functions have stationary values, and the corresponding value of y, and determine the character of the stationary point (max, min or point of inflection).
(a) y = 3 - x + x2 (b) y = x + 1/x
(c) y = 8 - x3 (d) y = 4x3 - x4
4. Differentiate the following (without multiplying out the terms!):
(a) x(x2 + 1) (b) 3x(5 - x ) (c) (x2 + 1)(3x3 -2x + 2)
(d) x(5x - 1)(7x2 + 4) (e) (x2 + 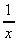 ) x (f)
) x (f) 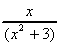
(g) 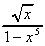 (h)
(h) 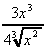
5. When isobutyl bromide and sodium ethoxide at equal concentration react in ethanol solution each concentration (C) is found to vary with time (t) according to the equation:
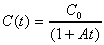 (1)
(1)where C0 is its initial concentration and A is a constant.
(a) Derive an expression for the rate of consumption of isobutyl
bromide or sodium ethoxide, given by 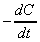 .
.
(b) If the reactant concentrations C0 are chosen to be 0.06 mol dm-3, and the temperature is 95ºC, C(t) falls to 0.05 mol dm-3 after 10 minutes. Use eqn.(1) to derive a value of A. Hence calculate the initial (t = 0) rate of consumption (in mol dm-3 min-1). What will be the concentrations after 25 minutes?
 To answers
To answers