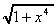 is a square root function of a quartic
function
is a square root function of a quartic
functionC. Function of a Function
Suppose we want to differentiate (2x -1)3.
We could expand the bracket then differentiate term by term,
but this is tedious! We need a more direct method for expressions
of this kind.
Now (2x-1)3 is a cubic function
of the linear function (2x -1), i.e. it is
a function of a function.
Other examples
(x2 - 3)3 is
a cubic function of a quadratic function
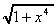 is a square root function of a quartic
function
is a square root function of a quartic
function
There are 2 ways to think about solving functions of a function:
(i) Chain Rule
If we have y(x) = f (complicated expression),
we let u = (complicated expression) then work out 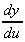 and
and 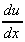 . We then use:
. We then use:
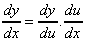 The Chain Rule
The Chain Rule
Examples
1. y = (2 - x3)4
let u = 2 - x3, so that y = u4
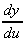 = 4u3 and
= 4u3 and
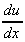 = -3x2
= -3x2
So 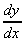 = (4u3).(-3x2)
= -12x2(2 - x3)3
= (4u3).(-3x2)
= -12x2(2 - x3)3
2. y(x) = 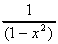 , i.e.
y = (1 - x2)-1
, i.e.
y = (1 - x2)-1
let u = (1 - x2), so that
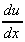 = -2x
= -2x
and y = u-1, so that 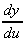 = -
= -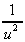
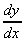 = (-2x)(-
= (-2x)(-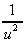 )
= +
)
= +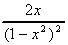
(ii) Sequential Step Method
With this method, we start with the outermost function, and differentiate
our way to the centre, multiplying everything together along the
way.
Examples
1. y = (2 - x3)4
think of this as y = (expression)4
differentiating, dy/dx = 4(expression)3
We now look at the expression in the brackets and differentiate
that (= -3x2) and multiply it to our previous answer to
give
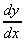 = 4(2 - x3)3(-3x2)
(which is the same as before)
= 4(2 - x3)3(-3x2)
(which is the same as before)
2. y = 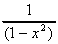 = (1 - x2)-1
= (1 - x2)-1
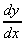 = -(1 - x2)-2
. (-2x)
= -(1 - x2)-2
. (-2x)
3. y = 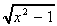 = (x2
- 1)½
= (x2
- 1)½
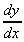 = ½(x2
- 1)-½ . 2x
= ½(x2
- 1)-½ . 2x
4. Refer back to this later, after we've covered sin and ln.
y = sin{ln(3x2 + 2)}
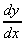 = cos{ln(3x2
+ 2)} .
= cos{ln(3x2
+ 2)} . 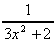 . 6x
. 6x
The general expression for an exponential function is
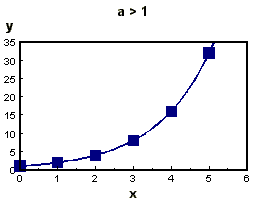
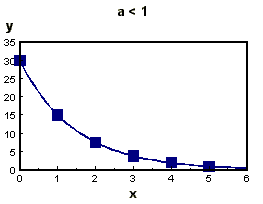
An example is y = 3x
| x | 0 | 1 | 2 | 3 | 4 | etc |
| y | 1 | 3 | 9 | 27 | 81 | etc |
One of the most important properties of an exponential function
is that the slope of the function at any value is proportional
to the value of the function itself.
In other words, 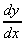 proportional to y(x),
or
proportional to y(x),
or  = constant
= constant ![]() y(x)
y(x)
the value of the constant depends upon the function y(x).
Numerical examples
1. y = 2x, plot the graph and measure
the slopes at different values of x.
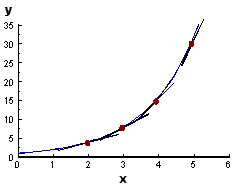
| x | y | slope at x measured from graph | slope / y |
|---|---|---|---|
| 0 | 1 | 0.69 | 0.69 |
| 1 | 2 | 1.38 | 0.69 |
| 2 | 4 | 2.76 | 0.69 |
| 3 | 8 | 5.52 | 0.69 |
| 4 | 16 | 11.04 | 0.69 |
So for y = 2x, the constant is 0.69 (later
on we'll see this is ln 2).
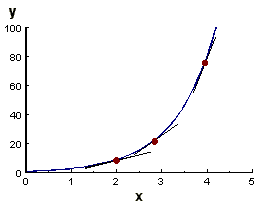
| x | y | slope | slope / y |
|---|---|---|---|
| 0 | 1 | 1.1 | 1.1 |
| 1 | 3 | 3.3 | 1.1 |
| 2 | 9 | 9.9 | 1.1 |
| 3 | 27 | 29.7 | 1.1 |
| 4 | 81 | 89.0 | 1.1 |
So for y = 3x, the constant = 1.1
Now, in the above 2 examples we used simple numbers (a
= 2 and a = 3), but the constants were not simple
numbers.
But we can reason that there must be some number between 2 and
3 for which the constant = 1, exactly.
i.e 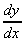 = y(x)
= y(x)
The value of a that gives this result is known as "e" and has the value:
an irrational number.
e is actually calculated from the following progression formula:
The Exponential Function
The function ex is known as the
exponential function (as opposed to any other exponential function)
and is extremely important in all branches of science:
What does ex look
like?
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| ex | 1 | 2.72 | 7.39 | 20.1 | 54.6 | 148 |
| e-x | 1 | 0.37 | 0.14 | 0.05 | 0.02 | 0.007 |
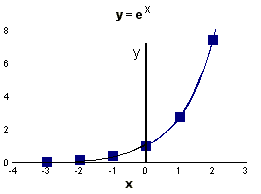
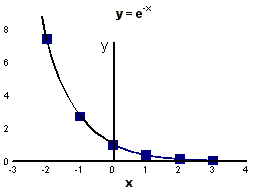
 Next lecture
Next lecture