Secular Equations and Secular Determinants

Equations 12 and 13 form the secular equations:

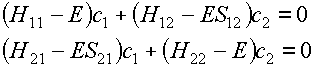(14)

These equation have a "trivial" and useless solution c₁= c₂ = 0. The condition that there should exist a nontrivial solution of these equations is that the secular determinant should be zero:

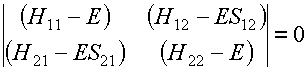(15)

Everything in this equation is a known number except E. The equation is therefore an equation for E. In the present case where the molecular orbital was a linear combination of just two atomic orbitals it is a quadratic equation and has two solutions for E. These two values of E are the molecular orbital energies. We always get the same number of molecular orbitals as atomic orbitals we start with.

Finding the MO energies by multiplying out the secular determinant