Combined quantum
mechanical/molecular mechanical (QM/MM) methods
·
To treat a chemical reaction, a quantum mechanical method is required
to describe the breaking and forming of bonds - such methods include ab initio
and semiempriical molecular orbital methods.
·
Molecular mechanics methods are not suitable, as outlined
above.
·
However, ab initio methods cannot be applied to systems with more
than a few tens of atoms, because the computational demands are too great.
·
Semiempirical methods can be applied to bigger systems (100s of
atoms), but even they are too demanding for calculations on very large
systems.
·
For calculations on reactions in solution, where thousands of
solvent molecules may need to be included, or for reactions in solids, at
surfaces or in biological macromolecules (e.g. enzymes), a different approach
must be used.
·
Quantum mechanical/molecular mechanical (QM/MM) methods allow
reactions in large systems to be studied.
·
A small region including the reacting atoms is treated with a QM
method (e.g. ab initio molecular orbital theory), while most of the system is
represented more simply by molecular mechanics.
·
The QM (e.g. reacting) region ‘feels’ the influence of the
molecular mechanics environment - for example, the atomic charges of the MM
atoms affect the QM atoms.
·
By combining the accuracy of a QM method (for a small reacting system)
with the speed of a MM method (for its surroundings), reactions in large
molecules and in solution can be studied.
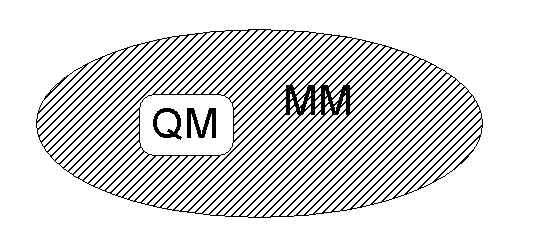
Schematic representation of the setup of a QM/MM calculation.
A small region
containing the reacting atoms is treated by a quantum mechanical method (e.g.
molecular orbital theory), and its surroundings are represented more simply by
molecular mechanics.
The total energy
of the system can be written as:
E= E(QM) + E(QM/MM) + E(MM) +
E(boundary)
· The energy of the QM system, E(QM), and
the energy of the MM system, E(MM) are calculated exactly as they would be in a
standard calculation at those levels.
· E(QM/MM) is the interaction energy between
the QM and MM regions (e.g. due to the interaction of the MM atomic charges
with the QM system)
· E(boundary) the energy due to any boundary
restraints applied to the outer edge of the MM region to maintain its
structure.
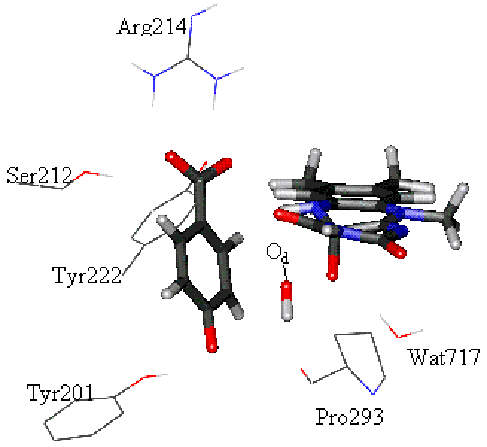
Modelling an
enzyme-catalysed reaction with a QM/MM method.
The picture shows the active site of
para-hydroxybenzoate hydroxylase, which hydroxylates (adds an OH group) to its
substrate, para-hydroxybenzoate. The
atoms treated by QM are shown as (thick) bonds. Other groups in the enzyme are
treated MM in the calculation (some of the important surrounding residues are
shown in thin lines). The transition state for hydroxylation is shown (Od
is being transferred from the flavin cofactor on the right, to form a new C-O
bond with the substrate (shown on the left).