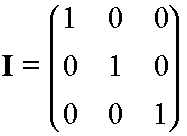Example of the application of the Newton-Raphson method to locating a minimum

To find the minimium of the function f(x,y)=x² + 3y², starting from the point x=4, y=5.

The Newton-Raphson expression for stepping towards a minimum (for a multidimensional function) is:

x_k+1 = x_k -gH^–1

g is the gradient (vector of first derivatives), H is the Hessian matrix (matrix of second derivatives).

H^–1 is the inverse of H. Remember that a matrix multiplied by its inverse gives the identity or unit matrix, I

A^–1A = I

The unit matrix, I, is a diagonal matrix in which all the diagonal elements are 1 (all off-diagonal elements are zero).

For example, the 3 ´ 3 unit matrix is:

Next: calculating the Hessian matrix