Example of locating a saddlepoint with the Newton-Raphson method

Remember that Newton-Raphson geometry optimization methods will converge to a saddlepoint if the starting structure is close to it (it should find the nearest stationary point).

For example, for the function

(1)

there are minima at (1,0) and (-1,0).

· We can use the Newton-Raphson method to step towards the saddlepoint between these minima if we start fairly close to it.

· We need the second derivative (Hessian) matrix), which is:

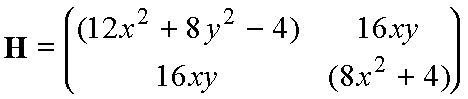(2)

At the point (x,y) = (1/4, 0):

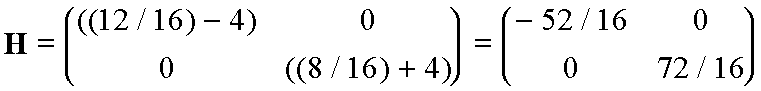(3)

So the inverse Hessian is:

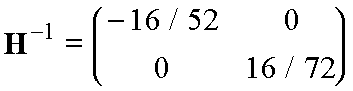(4)

The gradient (first derivatives) is:

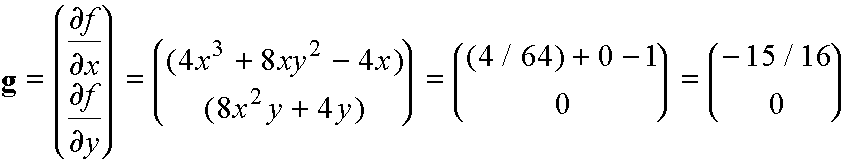(5)

Next: optimizing to a saddlepoint using the Newton-Raphson method (cont.)