The mass-weighted Hessian matrix is given by:
F = M–1/2HM–1/2 (4)
· M is a matrix
containing the atomic masses.
· Like the
Hessian matrix, H, it is a 3N ´ 3N matrix (N is the number of atoms).
· M is a diagonal matrix - the only non-zero elements are the
masses.
Finding the eigenvalues (li) of the mass-weighted Hessian matrix, F, gives the frequencies of the normal
modes, ni:
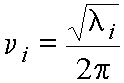 (5)
(5)
· If Cartesian
coordinates are used, there will be 3N
frequencies (from 3N eigenvalues),
where N is the number of atoms.
· Among these
frequencies, 6 will be very close to zero (5 for a linear molecule). These 6 correspond to overall translation
and rotation of the molecule.
· The remaining 3N-6 are vibrations of the molecule.