Example of a normal mode calculation: finding the vibrational frequency of a diatomic molecule

The potential energy is taken here to be harmonic,

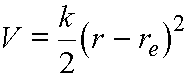(6)

where r is the separation of the two nuclei, and r_e their equilibrium separation.

· We can write this in terms of the Cartesian coordinates of the two atoms, x₁ (for atom 1) and x₂ (for atom 2) - we are taking the bond to lie along the x axis, and ignoring the y and z directions. Therefore, r = x₂-x₁.

· The second derivatives of the potential energy are:

d²V/dx₁² = k,

d2V/dx₂² = k,

d²V/dx₁dx₂ = d²V/dx₂dx₁ = –k.

· Therefore the Hessian matrix (for the x direction only here) is:

(7)

Next: the mass-weighted Hessian matrix and its eigenvalues