Molecular Simulation and Statistical Mechanics
∑
The energy calculated by molecular
mechanics or quantum mechanics corresponds to a state in which the nuclei are
at rest.†
∑
In reality, we need to take into account the
effects of temperature, and zero-point energy.
∑
In addition, laboratory measurements
are obviously not carried out at absolute zero on single molecules.† Experiments are done at higher temperatures
on large numbers of molecules.†
∑
We ideally need to include the vibrational, translational and
rotational energy at a particular temperature to compare with experimental
results.†
∑
To do this, the techniques of
statistical mechanics are used. Central to statistical mechanics is the partition function.
The vibrational frequencies from a normal
mode analysis can be used to find the zero-point energy of a molecule, as we
have already seen. More fundamentally, the calculated frequencies can be used
to calculate the (vibrational) partition function. All thermodynamic
properties can be calculated from the partition function, q:
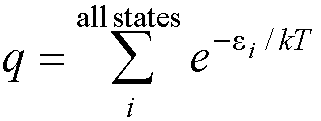
Where ei is the energy
of state i.
We can usually write the total energy
as the sum of translational, vibrational, rotational and electronic
contributions (see Prof. Balint-Kurtiís course, or Atkins Physical Chemistry, 6th edn., Chapter 20)
U = Utrans
+ Urot + Uvib + Uelec
which means that the partition
function can be factorized:
q = qtransqrotqvibqelec
and so we can
treat each contribution separately.†
∑
The translational partition function can be calculated using the
fact that the separation of translation energy levels is small.
∑
Usually for polyatomic molecules, the rotational partition function
can be found by similarly assuming the gaps between rotational energy levels
are small, and using the moments of inertia of the structure.
∑
Unlike the rotational and vibrational energy levels, the gaps
between the vibrational energy levels are not small compared to kT.†
We know that the vibrations of the molecule can be found by a normal
mode analysis - treating them as independent harmonic oscillators.† The energy levels of each mode are given by
the frequency, Ev = (v +
Ĺ)hn.† For a single harmonic oscillator.†
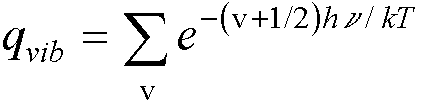
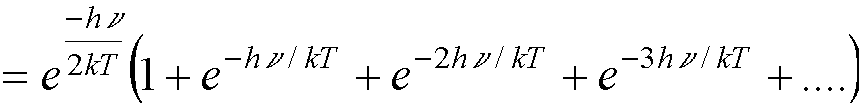
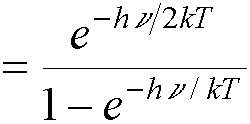
(because 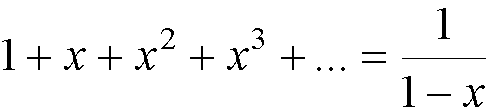 †).†
†).†
Each normal mode contributes a
partition function of this type, so the overall vibrational partition function
for a polyatomic molecule is the product of all of them:†
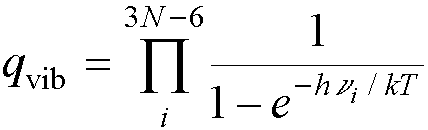
From a frequency calculation, we can calculate the vibrational
partition function of a molecule, and we can then use this to calculate the
thermodynamic properties of the molecule.†
The electronic partition function
involves summing over electronic quantum states (i.e. the lowest electronic
state and all excited states). Usually the gap between the electronic states is
very large, so only the ground state needs to be considered.