· All the thermodynamic properties of the molecule can now be calculated.

· Usually we are interested in calculating energy differences, not absolute energies.

· Free energy differences give equilibrium constants and rate constants.

· As you have seen in earlier courses, The equilibrium constant, K, for a reaction is related to the standard Gibbs free energy for reaction, D_rG^q :

·

D_rG^q = –RT ln K

· Calculations are more useful for studying rate constants than equilibrium constants (equilibrium constants can usually be measured straightforwardly experimentally or derived from tables of thermodynamic data – rate constants on the other hand depend on the properties of the transition state, and transition states are not easily studied by experiment).

· From transition state theory, rate constants may be expressed in terms of the activation free energy, D^‡G, (the free energy difference between reactants and the transition state), e.g. for a first-order reaction:

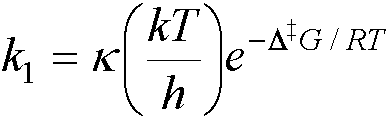
A standard activation enthalpy, D^‡H, and standard activation entropy, D^‡S, can be defined:

D^‡G = D^‡H – TD^‡S

· We have assumed that the total energy can be written as a sum of different terms (translational, rotational, vibrational and electronic). This is a good approximation.

· In exactly the same way, the enthalpy and entropy of a molecule can be written as a sum of contributions:

H = H_trans + H_rot + H_vib + H_elec

S = S_trans + S_rot + S_vib + S_elec

By calculating each of these terms for the reactant(s) and transition state of a reaction, we can calculate the activation free energy as D^‡G = D^‡H – TD^‡S. For one mole of a (non-linear) molecule in the gas phase, H_trans =5RT/2, H_rot= 3RT/2.

The vibrational enthalpy is given by:

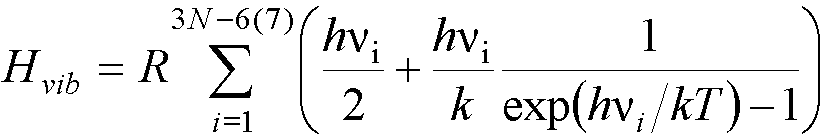
where k is again the Boltzmann constant.

· You don’t need to be able to remember this equation. You do need to notice (and be able to explain) a couple of things about it.

· First, the sum is over 3N-6 normal modes for a stable (non-linear) molecule, but over 3N-7 modes for a transition state.

· There is one less normal mode for a transition state because the motion along the reaction coordinate is not included as a normal vibration.

· Remember that in a normal mode analysis of a transition state, one of the modes has an imaginary frequency –this is the reaction coordinate, and is not included in the sum.

· The other thing to notice (and remember) about this expression is that it is made up of two parts, the first is the zero-point energy, and the second depends on the temperature. This is the contribution to the enthalpy from molecules that are not in the vibrational ground state.

There are similar expressions (again derived from the partition function) for the entropy.

The difference in enthalpy and entropy between the reactant(s) and transition states can them be calculated (e.g. for a bimolecular reaction, D^‡H_trans = -5/2RT (going from two moles of molecules (reactants) to one mole (transition state), similarly D^‡H_rot = -3/2RT).

Adding the enthalpy and entropy differences between the reactant(s) and the transition state gives the activation free energy D^‡G = D^‡H – TD^‡S.

Measuring relative to the energy of the reactants, the enthalpy of the reactants is zero, and that of the TS is DE^‡, the difference between the electronic energy of the reactants and the transition state (e.g. given by an ab initio calculation – remember that transition states cannot be modelled by standard molecular mechanics. Remember also that a method that includes electron correlation would be needed to calculate the energy of the transition state accurately).

Next: contributions to the activation free energy