So we can calculate the activation free energy D^‡G, activation enthalpy D^‡H and activation entropy D^‡S, broken down into rotational, vibrational, translational and electronic terms.

This gives insight into which factors are most important in determining the barrier to a reaction.

For example, for the Diels-Alder reaction:

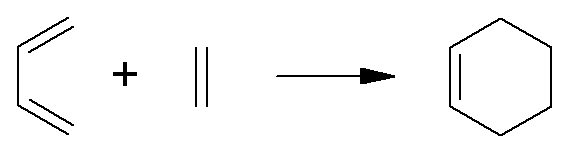
	D^‡H	–TD^‡S
electronic	74.9	0
vibrational	14.2	–6.7
rotational	–3.8	14.2
translational	–6.3	43.5
total	79.0	51.0

(in kJ mol^–1, at 300K).

For the S_N2 reaction of OH^– with CH₃F to form CH₃OH and F^–:

	D^‡H	–TD^‡S
electronic	21.3	0
vibrational	8.8	–8.8
rotational	–2.5	0.4
translational	–6.3	33.9
total	21.3	25.5

(in kJ mol^–1, at 300K)

For the Claisen rearrangement of allyl vinyl ether to form 5-hexenal:

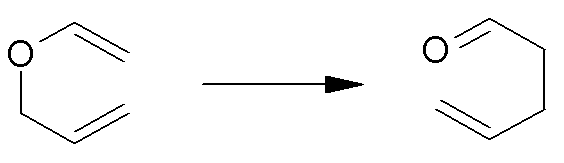
	D^‡H	–T^‡DS
electronic	97.9	0
vibrational	–5.4	10.9
rotational	0	0.4
translational	0	0
total	92.5	11.3

(in kJ mol^–1, at 300K)

· All these calculations used the MP2 method (e.g. with the 6-31G(d) basis set).

· In all these cases, the vibrational energy contribution includes the difference in zero-point energy between the reactants and the products.

· All of these contributions to the energy barrier can be found from the structure and energy of the reactants and TS, and from the partition functions.

· For example, the vibrational contribution can be found from the calculated harmonic frequencies (the TS has one less frequency).

· The energy gaps between translational levels, and between rotational levels, are very small, which means that these contributions can be calculated classically (e.g. each degree of freedom contributes RT/2 to the enthalpy). Remember that in a reaction like this, two molecules are coming together to form a single TS, so 3 rotational degrees of freedom and 3 translational degrees of freedom are lost going to the TS (for non-linear reactants). There is also a PV correction to the translational term, on going from 2 moles (reactants) to one mole (TS), i.e. PDV = DnRT = –RT (Dn = –1). Altogether this means that D^‡H_trans and DH_rot contribute –4RT per mole to D^‡H for a bimolecular reaction (of two non-linear molecules). The translational and rotational entropy changes are large and negative, opposing formation of the TS.

· For a unimolecular reaction, translation and rotation make no contribution to D^‡H (the number of rotational and translational modes, and the number of moles, is the same as for the reactants), and the entropy changes are small

· For all reactions, the vibrational contribution may be significant. The largest contribution to the barrier, however, is often the electronic energy difference between the reactants and the TS. This energy is the energy of the electrons and nuclei in the molecule, with the nuclei at rest. That is, the geometry of the molecule is fixed (at the minimum or TS structure). The electronic energy is the energy which is plotted on a potential energy surface diagram.

Next: summary, and solvent effects