Calculating activation free energies - summary

· To summarize, to calculate a rate constant, we need to calculate D^‡G.

· This can be done if we know the structure, energy and normal modes of the molecule.

· Remember there are approximations involved – e.g. treating all vibrations as harmonic, which as you know is a poor approximation for low energy, ‘floppy’ motions, and for internal rotations. The most important contribution to the barrier is usually the electronic energy.

· Barriers can be calculated to within approximately 0.1 kcal/mol only for very simple systems, and it is only at this level of accuracy that it is usually worth going beyond the harmonic oscillator approximation. It is difficult to calculate activation energies to within 1 kcal/mol.

· Even a calculation of D^‡G accurate to within 0.2 kcal/mol would give an error of a factor of 1.4 at 300K in a rate constant (recall the expression for a first-order rate constant above). This is worse than can be achieved by experiment for these simple systems.

· Calculations are more useful for understanding and predicting relative rates, e.g. predicting the effects of substituents, ratios between different possible products. They help with the interpretation of experiments. Also, calculations allow transition states and reactive intermediates to be studied directly (this is difficult by experiment, particularly for large molecules, and in condensed phases)

Solvent Effects

· The examples above are for small molecules in the gas phase.

· It is possible to include the effects of solvent in approximate ways (i.e. not including solvent molecules explicitly in a calculation).

· For example, in a quantum chemical calculation (e.g. ab initio, semiempirical or density-functional), solvation energy can be calculated by treating the solvent as a uniform medium with a dielectric constant e.

· The molecule occupies a cavity in the solvent (the simplest models use a sphere big enuogh to encompass the molecule, but better models use a cavity based on e.g the van der Waals radii of the atoms in the molecule, to define a cavity based on the molecular shape).

· A molecule’s solvation free energy can then be written as the sum of different terms:

DG_solvation = DG_cavity + DG_dispersion + DG_{electrostatic}

Creating the cavity within the solvent costs energy (DG_cavity), while there are favourable dispersion interactions between the solvent and the solute (DG_dispersion). These two terms are usually combined, and assumed to be proportional to the solvent-accessible surface area of the molecule. Different atom types are different parameters to relate the solvation energy to their solvent-exposed surface area.

The simplest estimate of the electrostatic component of the solvation energy (DG_{electrostatic}) is given by the Born model, which treats the cavity as a sphere for a molecule with charge q. The Onsager model is similar (a molecule is represented simply by its dipole). Better models include more complete representations of charge distribution in the molecule (e.g. based on the electrostatic potential), and also polarization due to the solvent.

· These methods are used in ab initio calculations because the computational demands of high-level calculations prevent (many) solvent molecules being included explicitly.

In molecular mechanics, one effect of solvation (the screening of charges) can be included approximately by altering the dielectric constant used in the calculation of electrostatic interactions – this reduces the interaction energy between charges q_i and q_j by the factor 1/e where e is the solvent dielectric constant.

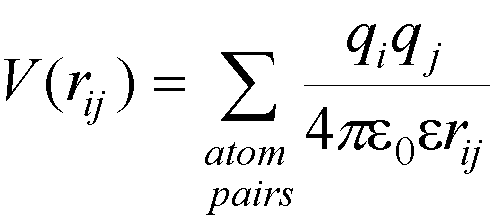
Alternatively, the dielectric constant can be made distant dependent (making the dielectric constant proportional to r), reducing the interaction energy two charges by 1/r where r is the distance between them, i.e.

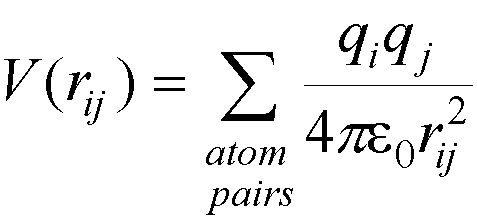
greatly reducing the interaction between different groups.

· However, these are highly approximate approaches.

· There are better ‘implicit solvent’ models for molecular mechanics, which can give good results, and allow large molecules to be treated in long simulations, while including solvation effects.

· Ideally though, we want to include solvent molecules explicitly.

Next: molecular simulations