Superconductivity Theory - Background

To explain the properties of superconductors, it is first neccesary to look at how normal conductors behave:

Electron Conduction Transport

Metals conduct electricity via delocalised electrons within the metal lattice - in a metal, the atoms lose valence electrons to form a lattice of positively-charged cations. The valence electrons are then delocalised throughout the lattice, and are free to move between the cations - these electrons are the current carriers.

The simplest way of explaining conductivity is by using the Drude model. The Drude model makes the assumption the conducting electrons

1. do not interact with the cations (the "free electron approximation"), except for collisions, where the velocity of the electron abruptly and randomly changes direction as a result of collision ("relaxation time approximation");

2. maintain thermal equilibrium throughout collisions ("classical statistics approximation");

3. do not interact with each other ("independent electron approximation").

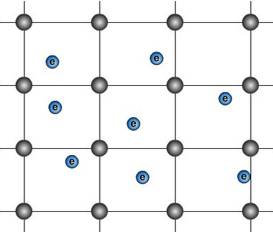Left: The Drude model approximates the metal to a lattice of cations through which delocalised electrons flow.

For our purposes, it is necessary to adopt a modified instance of the Drude model, whereby the electrons are assumed to have zero electrical potential between the cations, but near the cations the potential is negative - that is, the free electron approximation outlined above is not adopted.

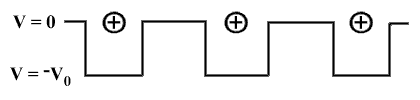Above: Abandoning the free electron approximation: the potential is negative near the cations and zero in the region between ions. (Reproduced from 'Superconductivity', Poole, Farach, Creswick, Academic Press, 1995)

Electron-Phonon Interaction

The cations within the lattice are oscillating about their equilibrium positions due to thermal energy. The resulting propagating lattice vibrations are called phonons, as they are essentially sound waves.
The electrons then interact with the cations as they move through the lattice - causing charge distortions that propagate along the lattice structure, in turn causing distortions in the periodic potential.

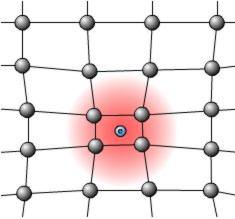Left: Lattice distortion around an electron causes an increase in positive charge density that will propagate along the lattice with the cation vibrations.

These distortions can affect the motion of another electron at some distance that is also interacting with the lattice in a similar way - this is thus called an electron-phonon interaction, and is an integral part of Cooper pair formation.
From this, it is simple to see why conductivity decreases with temperature - increased thermal energy will cause the cations to oscillate more violently; the electron-phonon interactions are greater and so impede the flow of electrons through the lattice. Conceptually, it is simplest to visualise this as the cations physically 'knocking' the electrons off their paths: