|
Thus far, we have been concerned with potential energy surfaces derived
under the Born-Oppenheimer approximation (see section
3.1), also known as the adiabatic approximation.
Hence, such surfaces are referred to as adiabatic
potential energy surfaces.
Avoided crossings are typical of adiabatic surfaces and arise because
the adiabatic electronic states corresponding to the surfaces are often
mixtures of two simple molecular orbital (i.e., covalent) or valence bond
(i.e., ionic) electronic structures (cf. the NaCl example used in section
11 to explain the non-crossing rule), where the original energy functions
do cross.
A surface where actual intersections are substituted for the avoided crossings
is termed a diabatic surface.
If the nuclei are assumed to move slowly, then they are likely to follow
a single, adiabatic energy surface, even in the region of an avoided crossing.
If the nuclei have sufficient velocity, then the Born-Oppenheimer approximation
breaks down and the nuclei may effectively “ignore” the gap
in the avoided crossing and simply cross over to the other adiabatic surface,
adopting that configuration. This is termed non-adiabatic
behaviour can be modelled, to some extent, by a diabatic representation.
Figure 12.1 goes someway to illustrating the adiabatic and diabatic representations
of a polyatomic surface:
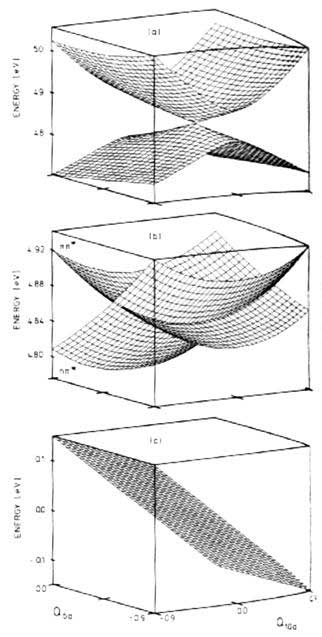 |
| Figure 12.1 - Close -up view of the
S1–S2
conical intersection in pyrazine in the Q6a–Q10a
space. Adiabatic surfaces are shown in (a), the diabatic diagonal
elements H11 (nπ*)
and H22 (ππ*)
are shown in (b). The diabatic coupling element H12
is shown in (c) [33] |
|