13.1 What is a conical intersection?
Figure 12.1 illustrates what we
will be concerned with in this section – a conical intersection
between (adiabatic) potential energy surfaces. Figure
13.1 (below) shows another view of this conical intersection.
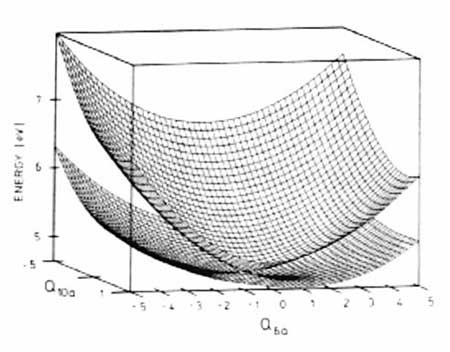 |
| Figure 13.1 - Conical intersection
of the adiabatic S1 and S2
PE surfaces in the two-dimensional space spanned by the tuning mode
Q6a
and the coupling mode Q10a[32] |
Conical intersections are interesting, firstly for the simple reason
that they exist – between adiabatic surfaces, where we would often
expect an avoided crossing. The distortion observed at a conical intersection
is a consequence of the breakdown of the Born-Oppenheimer separation.
At a conical intersection, one can distinguish two directions, X1
and X2, such that if the energy
in the subspace (the branching space) of these two geometric variables
(combinations of the bond lengths, angles, etc.), the potential energy
would have the form of a double cone in the region of the degeneracy.
The remaining n–2 directions define
the crossing surface (the intersection space) over which the energies
of ground and excited states are equal. A movement in the plane (X1,
X2) from a point on the intersection
will result in the degeneracy being lifted. The two vectors X1
and X2 correspond to the gradient
difference vector and non-adiabatic coupling vector, respectively. See
Figure 13.2 and equations (13.1) and (13.2) (below).
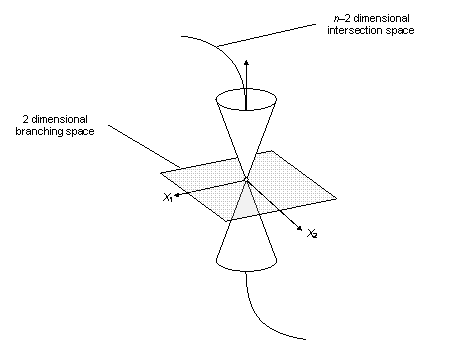 |
| Figure 13.2 - A conical intersection
as described by a double cone geometry using two variables, X1
and X2 |
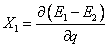 |
(13.1) |
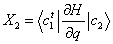 |
(13.2) |
The special case of a conical intersection is also sometimes termed a
Jahn-Teller distortion, following the
advent of the Jahn-Teller theorem concerning
such intersections in 1937.[34]
Conical intersections differ topologically from the accidental meeting
of energy surfaces – this is the essence of a Jahn-Teller distortion,
where it is shown that, for a conical intersection, the wavefunction changes
sign when transported (adiabatically) round a closed loop in the area
of the intersection.
The conclusion can be drawn from this that somewhere inside the loop,
there must be a single point where the wavefunction is degenerate –
i.e. a conical intersection, leading to a transition between surfaces.
Longuet-Higgins derived a topological test for locating a conical intersection
based on this principle, further using it as an argument as proof that
the non-crossing rule does not apply to polyatomics (the opposite of which
was suggested by Naqvi (see section 11).
The remarkable feature of Longuet-Higgin’s test is that it enables
one to locate the conical intersection purely from the wavefunction without
any prior knowledge of its existence.
This sign reversal in the wavefunction is often termed the geometric
phase (or Berry’s phase)
effect. Such non-adiabatic behaviour is, of course, not fully accounted
for by the Born-Oppenheimer approximation, yet it has been shown that
the geometric phase (GP) effect has a quantifiable effect on the reaction
probability in molecular scattering calculations at high energies, for
instance.
We have seen an example of a conical intersection present in pyrazine
(Figure 12.1 and Figure
13.1); conical intersections also exist in the H3 system,
the H4 system, HNO (H + NO), H+SiO, H+F2, ozone,
NO2, Li+H2, and HCN, to name but a few.
13.2 Features of conical intersections
We discussed, in section 12, the probability
of transitions between adiabatic surfaces at a near intersection, and
the diabatic representation of such crossings.
The main feature of a conical intersection is its non-adiabatic nature
– that is, that the breakdown of the Born-Oppenheimer approximation
allows non-adiabatic electronic transitions to take place. Clearly, it
is simple to visualise how an actual intersection facilitates easier transitions
than an avoided crossing. In fact, an actual intersection (i.e. a conical
intersection) allows radiationless decay (or non-absorbing when
considering the transition from lower to upper surfaces). This is illustrated
in figure 13.3:
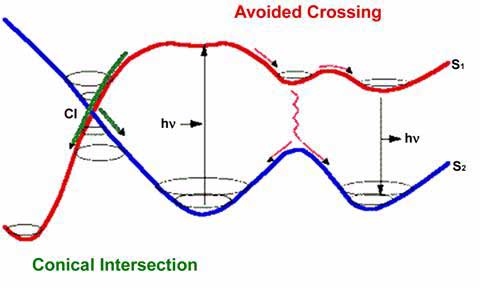 |
Figure 13.3 - Radiationless decay
at a conical intersection
(M.A. Robb, “What is a Conical Intersection?”, King’s
College, London) |
This is an important consideration in processes such as photodissociations,
isomerisations, charge-transfers, exchange collisions and energy transfers.
Worth and Cederbaum, for instance, have proposed the conical intersection
is an important feature in biological systems for the mediation of ultra-fast
electron transfers.[35]
Jimeno, et al. discuss conical intersections in a study of H+SiO
collisions, with reference to circumstellar SiO maser radiation, which
can be used in the identification of long-period variable stars.[36]
|
[34]
H.A. Jahn and E. Teller, Proc. Roy. Soc. Lond. Ser.
A., 161, 220, 1937
[35]
G.A. Worth and L.S. Cederbaum, “Mediation of Ultrafast Electron Transfer
in Biological Systems by Conical Intersections”, Chem.
Phys. Lett., 338, 219-223, 2001
[36] P. Jimeno,
M.D. Gray and G.G. Balint-Kurti, “Ab Initio Potential Energy
Surface for the Ground (2A') State
of H+SiO and Rotationally Inelastic Collision Cross Sections for Circumstellar
H+SiO Collisions”, J. Chem. Phys., 111,
4966, 1999 |