Computational enzymology: modelling the mechanisms of biological catalysts
Richard Lonsdale and Adrian J. Mulholland
Centre for Computational Chemistry, School of Chemistry, University of Bristol, Bristol BS8 1TS
Understanding how enzymes 'work' is a fundamentally important problem in biology. Enzymes are outstandingly efficient natural catalysts. Better understanding of the principles by which they achieve these catalytic properties is a central goal in the study of protein function. It also promises technological spin-offs such as routes to new drugs (e.g. in the design of enzyme inhibitors); analysis of the effects of genetic variation and mutation (e.g. in predicting the effects of single nucleotide polymorphisms on metabolism of pharmaceuticals); design of new catalysts (e.g. engineered enzymes or synthetic, designed biomimetic catalysts incorporating the same principles). There is great interest in developing protein catalysts for practical applications (e.g. in the pharmaceutical, chemical and biotechnology industries). Developments in systems biology will also require better quantitative understanding of enzyme action, e.g. for cellular network modelling, in the prediction of rates for individual biochemical reactions, and the effects of mutations on them. Modelling has a central role to play in these developments. Unstable species such as transition states and reaction intermediates are crucial to questions of reactivity, and cannot be studied directly by experiment in systems as complex as enzymes. Simulation and modelling allow enzyme catalytic mechanisms to be analysed in detail, and can contribute directly in catalyst design and protein engineering. Computational enzymology is a rapidly growing area, with modelling increasingly being recognised as essential for understanding these fascinating biological catalysts.1,2,3,4
Combined quantum mechanics/molecular mechanics (QM/MM) methods allow enzyme reactions to be modelled: a small region at the active site (where the reaction happens) is treated by a quantum mechanical electronic structure method, and interacts with the protein and solvent environment, which are included more simply (though in atomic detail) by an empirical 'molecular mechanics' force field. QM/MM methods combine the simplicity and speed of the MM treatment of the protein structure with the flexibility and power of a quantum chemical treatment (which allows modelling of bond breaking and making, and electronic polarization). QM/MM methods are becoming increasingly important in biomolecular modelling, in studies of enzyme mechanisms and other types of application. They were the topic of a recent CCP-BioSim training workshop (www.ccpbiosim.ac.uk ; see also ref. 41, Lonsdale et al. Chem. Soc. Rev. 2012, for a practical introduction).
Molecular mechanics (MM) methods give a good description of protein structure and interactions, and are very useful for molecular dynamics simulations. Standard MM methods cannot be used to model reactions, though. Potential functions of this type cannot be applied to model the bond breaking and bond making, and electronic reorganization, involved in a chemical reaction: the bond terms do not allow bonds to break or form, and electronic redistribution is not be accounted for. Also, the MM force field parameters are based on the properties of stable molecules, and so will usually not be applicable to transition states and intermediates formed during reactions. Quantum mechanical (QM) methods, on the other hand, can give accurate results for small molecules and their reactions. The major problem with electronic structure calculations on enzymes is that they require large computational resources required, which significantly limits the size of the system that can be treated. Quantum chemical methods (for example ab initio molecular orbital or density-functional theory calculations) can currently be used practically to study reactions in systems containing perhaps tens of atoms. Small 'cluster' models of around this size can represent important active site groups, and can identify likely mechanisms. Ideally, though, simulations should include the effect of the enzyme on the reaction, and so study larger models. This can be done using QM/MM methods, which can now offer unprecedented levels of accuracy for enzyme reaction barriers5, comparable to experiment.
Enzyme mechanisms, and the basic sources of their catalytic power, remain controversial. The first question to answer in studying an enzyme-catalysed reaction is 'what is the mechanism of the reaction'? This means identifying all the catalytic residues (and other catalytic groups, e.g. cofactors) and their roles, and establishing the structure of any reaction intermediates and transition states. Identifying the chemical mechanisms of enzymes by experiments alone is very difficult: it is often hard to differentiate between alternative proposed mechanisms. Many mechanisms given in standard biochemistry textbooks are probably incorrect in important details. Once the mechanism is known, the next challenge is to understand why the enzyme is a good catalyst, i.e. why the enzyme reaction is fast. Many enzymes have reaction rates which are many orders of magnitude faster than equivalent uncatalysed reactions in solution. Many different ideas have been put forward to explain these very large rate accelerations. These proposals, some well founded and some less so, are the centre of vigorous ongoing debates in enzymology about the origins of catalysis in some or all enzymes. These arguments are very difficult to settle, because the complexity and large size of enzymes makes experimental analysis very difficult. Examples of these controversies include the possible role of protein dynamics in driving catalysis2,3, 'low-barrier' hydrogen bonds6,7,8,9, 'near-attack conformations' 10,11, quantum tunnelling12 and the contribution of entropy3. These arguments have included questioning the applicability of transition state theory (a basic tool from chemical physics for understanding molecular reaction rates) for enzyme reactions2.
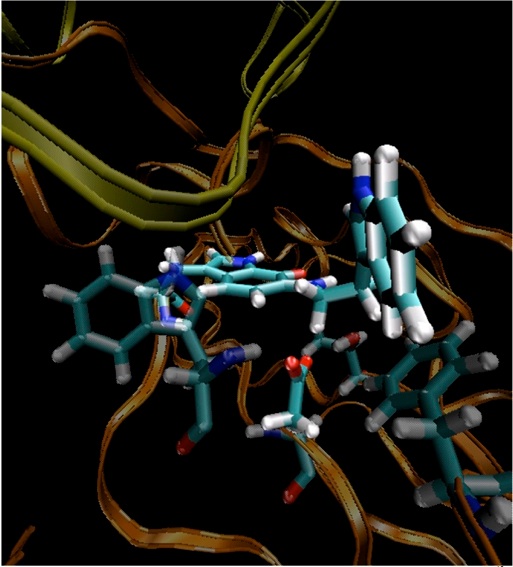

Modelling of enzyme reactions also promises to make a significant practical contribution in areas such as drug discovery. Many enzymes are drug targets (many pharmaceuticals are enzyme inhibitors), and ligand design should significantly benefit from knowledge of their mechanisms. By showing how transition states and reaction intermediates are stabilized in enzymes, mechanistic modelling can help inhibitor design, adding another dimension to structure-based ligand design for enzyme targets. For example, β-lactamase enzymes, which break down antibiotics, are a major cause of the growing clinical problem of bacterial antibiotic resistance. QM/MM modelling of the TEM1 β-lactamase from E. coli showed how the entire process of antibiotic breakdown can happen in the enzyme13,14. The results identified important interactions in the protein, and suggested modifications of existing β-lactam antibiotics that could improve their stability against lactamases, and so could provide a route to overcoming bacterial antibiotic resistance.
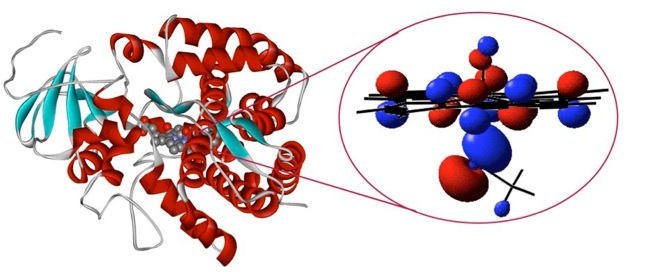

Until recently, QM/MM investigations of enzymes have generally been limited to relatively low levels of QM theory, such as semiempirical methods or density functional theory (DFT). Semiempirical methods are computationally cheap, fast enough for QM/MM molecular dynamics simulations, but are prone to significant errors. For example, reaction energies and barriers calculated with semiempirical QM methods can be wrong by 10 kcal/mol or more. DFT (especially with the B3LYP hybrid functional) offers improved accuracy, and has allowed computational studies of new classes of enzymes (particularly metalloenzymes such as cytochrome P450)23. DFT methods, however, lack key physical interactions, such as dispersion, which are important in the binding of ligands to proteins.24,25 DFT often gives barrier heights that are too low by several kcal/mol, and it does not offer a route to their systematic improvement or testing, making it difficult to assess the accuracy of results. Other modelling methods such as the empirical valence bond technique can give excellent results for enzyme activation energies3,26, and have provided important insight into the basic causes of catalysis. Such empirical approaches, though, require extensive fitting to experimental data, and do not consider the electronic structure explicitly. The 'gold standard' of quantum chemistry is provided by first principles – 'ab initio' – methods that include the effects of correlation between electrons. They allow calculations of rate constants with an accuracy similar to experiments, but only for molecules containing very few atoms, in the gas phase27. Previously, such accurate methods were limited to small molecules because of their enormous computational expense, which increases quickly as the size of the system increases. Using recent theoretical developments28 it is now possible to treat systems of the size of typical QM regions in QM/MM calculations on enzymes (for example, typically 25 to 50 atoms). Using such high-level ab initio methods, accuracy comparable to experiment can be achieved in QM/MM calculations on enzyme-catalysed reactions5. Calculated activation energies for two enzyme reactions (chorismate mutase and para-hydroxybenzoate hydroxylase) agree very well with experiment. The agreement with experiment indicates that transition state theory provides a good general framework for understanding the rates of such enzyme-catalysed reactions. These results show that reaction barriers in enzymes can be calculated with QM/MM methods with an accuracy of around 1 kcal/mol (so-called chemical accuracy) in the best cases. Biomolecular modelling can now deliver quantitative comparisons with experiment for enzyme-catalysed reactions, and make reliable predictions of enzyme mechanisms. This transforms what can be achieved by calculations and signals a new era in computational biochemistry.
The importance of simulations in understanding biological catalysts is certain to continue to grow: modelling will increasingly become an integral part of enzymology29,30,31,32,33,34,35,36,37,38,39,40. For an introduction to modelling enzyme-catalysed reaction mechanisms, see 'A practical guide to modelling enzyme-catalysed reactions' Lonsdale et al. Chem. Soc. Rev. 41, 3025-3038 (2012); http://dx.doi.org/10.1039/C2CS15297E.41
Acknowledgements
AJM thanks his co-workers in the work described here, and thanks EPSRC, Pfizer, Vernalis, BBSRC, NIH and the IBM High Performance Computing Life Sciences Outreach Programme for funding. CCP-BioSim is the UK Collaborative Computational Project for Biomolecular Simulation, see www.ccpbiosim.ac.uk.
References
1 Lonsdale R, Ranaghan KE, Mulholland AJ: Chem. Commun. 2010, 46: 2354.
2 Glowacki DR, Harvey JN, Mulholland AJ: Nature Chem. 2012, 4: 169.
3 Kamerlin SC, Warshel A: Proteins 2010, 78: 1339.
4 Senn HM, Thiel W: Angew. Chem. Int. Ed. Engl. 2009, 48: 1198.
5 Claeyssens F, Harvey JN, Manby FR, Mata RA, Mulholland AJ, Ranaghan KE, Schütz M, Thiel S, Thiel W, Werner H-J: Angewandte Chemie Intl. Edn. 2006, 45: 6856.
6 Cleland WW, Frey PA, Gerlt JA: J. Biol. Chem. 1998 273: 25529.
7 Mulholland AJ, Lyne PD, Karplus M: J. Am. Chem. Soc. 2000, 122: 534.
8 Schutz CN, Warshel A: Proteins: Structure, Function, Bioinformatics 2004, 55: 711.
9 Molina PA, Jensen JH: J. Phys. Chem. B 2003, 107: 6226.
10 Hur S, Bruice TC: J. Am. Chem. Soc., 2003, 125: 10540.
11 Strajbl M, Shurki A, Kato M, Warshel A: J. Am. Chem. Soc. 2003, 125: 10228.
12 Masgrau L, Roujeinikova A, Johannissen LO, Hothi P, Basran J, Ranaghan KE, Mulholland AJ, Sutcliffe MJ, Scrutton NS, Leys D: Science 2006, 312: 237.
13 Hermann JC, Hensen C, Ridder L, Mulholland AJ, Höltje H-D: J. Am. Chem. Soc. 2005, 127: 4454.
14 Hermann JC, Ridder L, Höltje H-D, Mulholland AJ: Org. Biomol. Chem., 2006, 2: 206.
15 Schoneboom JC, Cohen S, Lin H, Shaik S, Thiel W: J. Am. Chem. Soc., 2004, 126: 4017.
16 Guallar V, Baik M-H, Lippard SJ, Friesner RA: Proc. Natl. Acad. Sci. USA, 2003, 100: 6998.
17 Zurek J, Foloppe N, Harvey JN, Mulholland AJ: Org. Biomol. Chem., 2006, 4: 3931.
18 de Groot MJ, Kirton SB, Sutcliffe MJ, Curr. Topics Med. Chem., 2004, 4: 1803.
19 Pirmohamed M, Park BK: Toxicology, 2003, 192: 23.
20 Bathelt CM, Zurek J, Mulholland AJ, Harvey JN: J. Am. Chem. Soc., 2005, 127: 12900.
21 Bathelt CM, Ridder L, Mulholland AJ, Harvey JN: Org. Biomol. Chem., 2004, 2: 2998.
22 Lonsdale R, Oláh J, Mulholland AJ, Harvey JN: J. Am. Chem. Soc. 2011, 133: 15464.
23 Himo F, Siegbahn PEM: Chem. Rev. 2003, 103: 2421.
24 Lonsdale R, Harvey JN, Mulholland AJ: J. Chem. Theory Comput., 2012, 8: 4637.
25 Lonsdale R, Harvey JN, Mulholland AJ: J. Phys. Chem. Lett., 2010, 1: 3232.
26 Bjelic S, Åqvist, J: Biochemistry 2004, 43: 14521.
27 Wu T, Werner H-J, Manthe U: Science 2004, 306: 2227.
28 Manby FR, Werner H-J, Adler TB, May AJ: J. Chem. Phys. 2006, 124: 094103.
29 Ranaghan KE, Mulholland AJ: Int. Rev. Phys. Chem. 2010, 29: 65.
30 Ranaghan KE, Mulholland AJ: Interdiscip. Sci. Comput. Life Sci. 2010, 2: 78.
31 van der Kamp MW, Shaw KE, Woods CJ, Mulholland AJ: J. R. Soc. Interface 2008, 5: S173.
32 McGeagh JD, Ranaghan KE, Mulholland AJ: Biochim. Biophys. Acta 2011, 1814: 1077.
33 Lodola A, Mulholland AJ Methods Mol. Biol. 2013, 924: 67.
34 Roca M, Aranda J, Moliner V, Tuñón I: Curr. Opin. Chem. Biol. 2012, 16: 465.
35 Shaik S, Cohen S, Wang Y, Chen H, Kumar D, Thiel W: Chem. Rev. 2010, 110: 949.
36 Kamerlin SC, Warshel A: Phys. Chem. Chem. Phys. 2011, 13: 10401.
37 Lodola A, De Vivo M: Adv. Protein Chem. Struct. Biol. 2012, 87: 337.
38 Siegbahn PE, Himo F: J. Biol. Inorg. Chem. 2009, 14: 643.
39 Goyal P, Ghosh N, Phatak P, Clemens M, Gaus M, Elstner M, Cui Q: J. Am. Chem. Soc. 2011, 133: 14981.
40 Stansfeld PJ, Sansom MS: Structure 2011, 19: 1562.
41 Lonsdale R, Harvey JN, Mulholland AJ: Chem. Soc. Rev. 2012, 41: 3025.
