 Modelling CVD diamond growth
Modelling CVD diamond growth
Many researchers in the late '80s, early '90s developed a model for the growth of CVD diamond from hydrogen-rich gas mixtures. This so-called 'standard model' has been very successful, and still stands as a robust and (we believe) mostly correct description of the main processes leading to diamond growth. However, it has limitations: it cannot predict growth rates very accurately, nor can it predict the sizes of crystallites that may be present within the film. The standard model also runs into difficulties for some of the more extreme gas chemistries that are nowadays being used for high rate single crystal diamond growth, or for UNCD growth. Therefore, we have been working towards trying to improve the standard gowth model, to make it a universal description of CVD diamond growth that's applicable to all diamond growth regimes - a 'grand unified theory' for CVD diamond.
The standard growth model
This assumes that H2 is in large abundance within the gas mixture, and the action of the hot filament or MW plasma is to dissociate this into H atoms. Thus, the growing diamond surface is surrounded by a 'sea of H atoms'. These reactive atoms react with the H's which terminate the diamond surface to form H2, leaving behind a surface radical (dangling bond). The most likely fate for this dangling bond - given the high concentration of H atoms nearby - is that an H simply attaches to it, stabilising the surface, and the excess bond energy is dissipated into the surface as heat. Thus, the number of dangling bonds on the diamond surface at any one time is a function of the equilibrium between H abstraction and H addition reactions, which are both sensitive functions of the substrate and gas temperatures. We have derived an expression for the fraction R, of the surface covered in dangling bonds sites, as:
R = 1 / {1 + 0.3exp(3430/Ts) + 0.1exp(-4420/Ts)![]() [H2]/[H] } (1)
[H2]/[H] } (1)
where Ts is the substrate temperature. Thus, you can see that the hydrogen dissociation ratio, [H2]/[H], at the growing surface is a crucial parameter in determining the equilibrium number of surface radical sites that are present. Under typical CVD diamond conditions, R~0.1, i.e. there will be around 10% of the diamond surface with these dangling bonds.
However, occasionally, instead of an H atom, a CH3 radical (created in the plasma or near the filament by reactions between CH4 and H atoms) can add to a surface radical site, so adding one carbon to the lattice. This 'pendant' (dangling) CH3 group, however, is quite vulnerable, and can easily be etched or desorb back into the gas phase, in which case we are back to square one. But if the process of H abstraction, dangling bond creation, and CH3 addition, were to occur again, on a site adjacent to the pendant CH3, then there's the possibility that the new carbons can link up, and finally be locked into the lattice. This would propagate the diamond lattice, as shown in the diagram below.
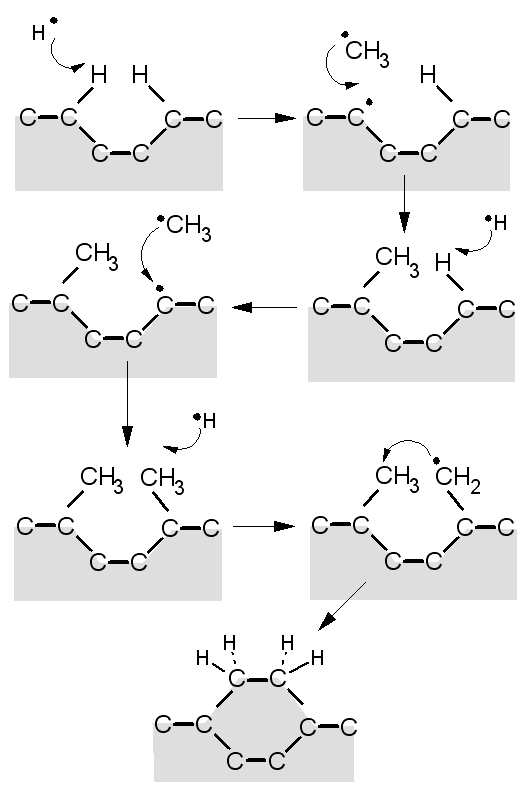
A schematic diagram of a simplified version of the Standard Growth Model for CVD diamond.
A video animation showing how a CH3 adsorbs and s then incorporated into the diamond lattice is available from Youtube.
An improved model for growth
In collaboration with Yuri Mankelevich from Moscow State University, we have developed a more detailed model for growth, in which we simply extend the ideas present in the standard model, but with a few extra features added. We assume that only C1 species (CH3, CH2, CH and C atoms) are involved in growth, so species such as C2, C2H, or larger hydrocarbons are ignored - mainly on the grounds of their small concentration. The C1 species, particularly CH3, are more abundant at the growing diamond surface by several orders of magnitude than these higher hydrocarbons.
 Our model considers only the (100)-(2×1) reconstructed surface, because growth on this surface is the most commonly studied. Experimentally, it has been found that under the same conditions the growth rates on many diamond surfaces, e.g., (100), (111) (110), (113) are very similar to each other (often less than a factor of ~2 difference), which suggests that our derived growth rate formulas for the (100)-(2×1) surface are valid for other diamond surfaces, including randomly oriented polycrystalline diamond, within a factor ~2.
Our model considers only the (100)-(2×1) reconstructed surface, because growth on this surface is the most commonly studied. Experimentally, it has been found that under the same conditions the growth rates on many diamond surfaces, e.g., (100), (111) (110), (113) are very similar to each other (often less than a factor of ~2 difference), which suggests that our derived growth rate formulas for the (100)-(2×1) surface are valid for other diamond surfaces, including randomly oriented polycrystalline diamond, within a factor ~2.
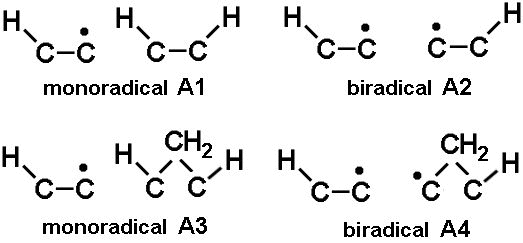
Although there are lots of different geometries for the surface radical sites, we assume they can all be categorised into 2 main classes. Monoradical sites have a single dangling bond, and biradical sites have two dangling bonds on adjacent carbons. From equation (1), if R~10% for monoradical site density under normal CVD conditions, R2 is the biradical site density ~1% - and will again be a sensitive function of temperature. The 2 types of site can be subdivided into types A1-4, depending on whether they are next to a bridging CH2 or not, as shown in the figure, right).
In our model, we assume that CH3 can add to both mono and biradical dimer sites, but CH3 cannot add to bridge and dihydride surface sites because of the strong steric repulsion among H atoms of the CH3 group and the surrounding surface H atoms. The different growth rates and observed crystal sizes are a direct result of the CH3 adding to the surface by different reaction channels.
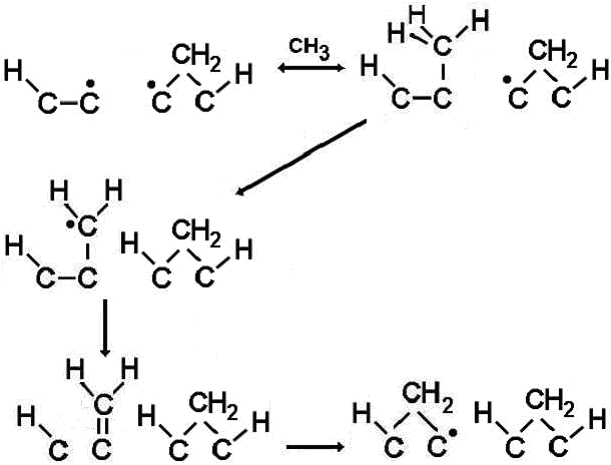 (a) CH3 addition to biradical sites
(a) CH3 addition to biradical sites
Since the biradical sites have an adjacent dangling bond already present, the CH3 adduct does not have to wait for a suitable abstraction reaction to occur before it can link into the lattice (see figure, right). Thus, the reaction that forms a bridging CH2 group readily occurs before the CH3 can desorb. We derived an equation for the growth rate contribution, G (in μm h-1) from CH3 via this biradical channel as:
Gbi = 3.8×10-14 Ts0.5 [CH3] R2 (2)
where Ts is the substrate temperature in K and R is the fraction of surface monoradical sites from Eqn.1.
(b) CH3 addition to monoradical sites
CH3 can also attach to monoradical dimer sites thereby terminating the single 'dangling bond' and forming a pendant CH3 adduct (see figure, below). There are then two competing processes which determine the fate of this adduct. One is that the adduct can simply desorb back into the gas phase (which is likely to be quite a facile process) and reform the monoradical site, and this can be quantified by a desorption rate, kd. Alternatively, a suitable H abstraction reaction might occur on a neighbouring lattice position (or on an H atom from the CH3 adduct) during the time the CH3 remains attached to the surface, followed by fast H atom transfer from the pendant CH3 to this vacant site. This H abstraction reaction would depend upon the gas-phase atomic hydrogen concentration above the surface, [H], and the rate would be given by ka[H], where ka is the rate constant for abstraction. Then, the pendant CH2 will create a dangling bond on the adjacent carbon of the same dimer via a β-scission reaction and thus, the pendant CH2 will be incorporated into the lattice as a bridging CH2 group. Therefore, for successful incorporation of CH3 into the diamond lattice via monoradical sites, the rate of H abstraction must be comparable with or higher than the CH3 desorption rate, i.e. ka[H] > kd. There are now two monoradical channels to compete with the biradical growth rate given by Eqn.(2). These channels involve two main monoradical sites during regular growth, a dimer-dimer pair (A1, above) and a dimer-bridge pair (A3, above). We also assume that the time-averaged fraction of these sites are 50%. To derive an expression for the growth rate, Gmono, via monoradical dimer channels similar to that in Eqn.(2), we change R2 (the probability of the surface site becoming a biradical site) in Eqn.(2) to R (the probability of the monoradical surface site), and multiply by the probability of CH3 incorporation via monoradical channels, given by ka[H] / (ka[H] + kd). Thus, we will have
Gmono = 3.8×10-14Ts0.5[CH3]R×0.5×ka[H] { 1/(ka[H]+kd(A1))+ 1/(ka[H]+kd(A3)) } (3)
and the total growth rate due to CH3 can now be expressed as:
GCH3 = 3.8×10-14Ts0.5[CH3]×R×{ 0.5×ka[H]×( 1/(ka[H]+kd(A1))+1/(ka[H]+kd(A3)) ) + R} (4)
where kd(A1) and kd(A3) refer to the rates of desorption of CH3 from A1 and A3 sites, respectively.

(c) Growth from CHx, x=0,1,2
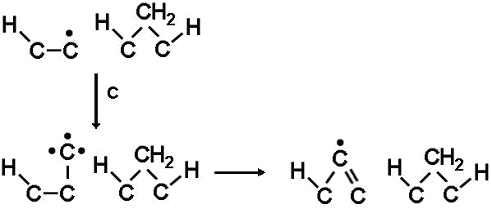 Although the concentratiopn of the other C1 species is usually much lower than that of CH3 at the growing surface, under some deposition conditions it can become 5%-10% of that of CH3. Thus, these species must not be neglected when modelling growth. CHx species, being more reactive than CH3, can readily attach to both surface monoradical sites and biradical sites. The C and CH radicals also differ from CH3 in that after bonding to the surface they still have at least one 'spare' dangling bond and thus remain highly reactive. In the case of monoradical sites, once attached, the reactive adduct does not have to wait for a subsequent H abstraction reaction, it simply utilizes its spare dangling bond to react with an adjacent carbon and link into the lattice (see figure, right). This will also occur on biradical sites in much the same way. Therefore, CHx species can be readily incorporated into the diamond lattice via both monoradical and biradical sites. The result of this is that even for low CHx concentrations, their contribution to the growth rate can become important since they can readily add to the more abundant radical sites.
Although the concentratiopn of the other C1 species is usually much lower than that of CH3 at the growing surface, under some deposition conditions it can become 5%-10% of that of CH3. Thus, these species must not be neglected when modelling growth. CHx species, being more reactive than CH3, can readily attach to both surface monoradical sites and biradical sites. The C and CH radicals also differ from CH3 in that after bonding to the surface they still have at least one 'spare' dangling bond and thus remain highly reactive. In the case of monoradical sites, once attached, the reactive adduct does not have to wait for a subsequent H abstraction reaction, it simply utilizes its spare dangling bond to react with an adjacent carbon and link into the lattice (see figure, right). This will also occur on biradical sites in much the same way. Therefore, CHx species can be readily incorporated into the diamond lattice via both monoradical and biradical sites. The result of this is that even for low CHx concentrations, their contribution to the growth rate can become important since they can readily add to the more abundant radical sites.
In a similar to manner to before, it is possible to estimate the contribution to the growth rate, G (in μm h-1), of these CHx species:
GCHx = 3.9×10-14 Ts0.5 [CHx] R (5)
where CHx is for x = 0,1,2.
(d) Total growth rate
The total growth rate will be obtained by the sum of the all the contributions:Gtotal = GCH3 + GCHx (i.e. Eqn(4) + Eqn(5)) (6)
(e) The fate of CH2 bridging groups, and crystal size estimation
From the stable bridging structure shown in (b), above, further hydrogen abstraction reactions allow the CH2 groups to migrate across the dimer chains (see movie of a simulation of this process) until they meet another CH2 bridge group or a step-edge, at which point they will lock into place, extending the diamond lattice, leading to large regular crystals. In contrast, many of the bridging structures created following addition of C and CH species (as shown in (d)) would remain reactive since they still contain at least one dangling bond. The most likely fate for such reactive surface sites, considering that they are surrounded by a gas mixture containing a high concentration of H atoms, is that they are rapidly hydrogenated to CH2. If so, the subsequent reactions will be indistinguishable from attachment and growth by methyl, as described above.
When the atomic H concentration is low, other fates for the reactive surface adducts become possible, such as reaction with other gas-phase hydrocarbon radicals (such as CHx and more complex species CyHz, y>1), further bridging, or cross-linking, which may lead to restructuring of the surface, or even renucleation of a new, misoriented crystallite. These processes are proposed to be one route by which the size of crystallites is prevented from becoming larger.
For the typical conditions used to deposit MCD/NCD and UNCD in a variety of different diamond CVD reactors (including MW and HF CVD reactors), the reactions of the surface adducts with atomic hydrogen which lead to continuous normal diamond growth are much more frequent events than the surface reactions which might ultimately lead to renucleation. So long as the surface migration of CH2 (induced by H abstractions) is much faster than adsorption of CH3, the aggregation of CH2 bridge sites into continuous chains (void filling) will provide normal layer-by-layer {100} diamond growth. But as the ratio of gaseous CHx/H increases, the initiation of next layer growth could proceed before all the voids in the current layer are filled. Thus, the average equilibrium crystal sizes, d, and hence the morphology of the subsequent film, will depend upon the relative concentrations of various species (H, H2, CHx, CyHz) close to the growing diamond surface, the probability of the renucleation events, and the deposition and pre-deposition conditions (e.g. nucleation density).
Comparing the frequency of CH2 surface migration processes with those for CHx addition we proposed a formula for <d> which could at least provide a first approximation to crystal size. Taking into account renucleation due to CHx and CyHz, an equation for the average crystal size <d> in nm can be given in the following general form:
<d> = { 2 + 0.6 exp(3430/Ts)} × ([H]/Σ[CHx])2 (7)
We should make it clear that the value of <d> calculated here would be the equilibrium, ultimate or limiting value that would be achieved after the growth had occurred for sufficient length of time that any effects due to the substrate material, surface topology, and nucleation methods can be neglected. When columnar growth occurs, such as during MCD deposition, the crystal size increases with growth time. Thus, in comparing our predictions with experimental data, we must be careful to ensure that the growth time was sufficiently long that that an equilibrium between the rate of secondary nucleation and the rate of crystal size increase had been reached. For UNCD, cauliflower NCD and SCD, this is not an issue since columnar growth does not occur and crystallite size is independent of growth time.
The figure below shows the predictions of Eqn.(7) as a function of [H]/Σ[CHx] plotted on a log-scale to allow all the diamond growth regions to be displayed on the same graph. The figure demonstrates that the type of film (SCD, MCD, NCD or UNCD) is determined simply by the [H]/Σ[CHx] ratio near the growing diamond surface. Low [H]/Σ[CHx] ratios will favour smaller crystal sizes, and thereby promote UNCD and NCD deposition. For [H]/Σ[CHx] values higher than ~3, the crystal size approaches a few μm, so this is the MCD regime. And, extrapolating the graph, for [H]/Σ[CHx] > ~60 the crystallite size becomes >100 μm, which is approaching SCD.
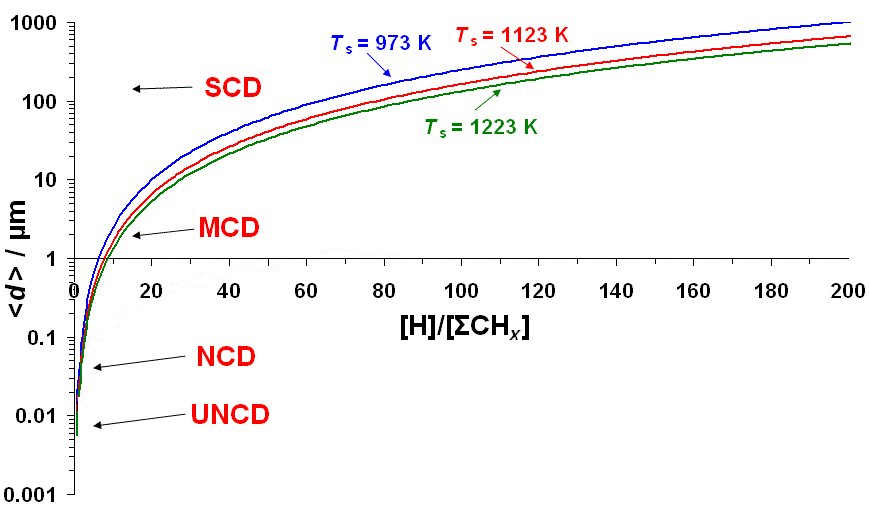
Values for the required parameters, such as gas temperature, and the concentrations of the various species at the growing diamond surface can be calculated using a sophisticated model of the gas phase chemistry within a reactor. When this is performed for the various process conditions used to grow the different types of diamond film, we find a remarkable agreement between the experimental values and predictions of the growth rates (Eqn.(6)) and the crystal sizes (Eqn.(7)). We can deduce that growth of diamond is a sliding scale, with different types of diamond arising from a smoothly changing ratio of atomic H to hydrocarbon radicals at the growing surface. The different growth conditions, gas mixtures, temperatures and pressures reported in the literature for diamond growth, simply serve to fix the value of this ratio [H]:[ΣCHx], and with it, the resulting film morphology and growth rate.
Although these findings seem to indicate that growth of all types of diamond can now broadly be explained, a word of caution is advised. We have not considered the effects of nitrogen upon either the gas chemistry or upon the surface reactions. Nitrogen, even as an unwanted impurity at the ppm level, is known to significantly effect growth rates and film morphology. Nor have we considered oxygen-, halogen-, or boron-containing gas mixtures, which also affect many aspects of growth. Nevertheless, we feel that the results in this paper give a valuable insight into the physical and chemical processes underlying diamond growth, and hopefully will provide some pointers to advance this technology further, in terms of higher growth rates, with higher purity, and larger crystals.
References:
- P.W. May, J.N. Harvey, J.A. Smith, Yu. A. Mankelevich, "Re-evaluation of the mechanism of ultrananocrystalline diamond deposition from Ar/CH4/H2 gas mixtures", J. Appl. Phys. 99 (2006) 104907.
- P.W. May, Yu. A. Mankelevich, "Microcrystalline, nanocrystalline and ultrananocrystalline diamond chemical vapor deposition: Experiment and Modeling of the factors controlling growth rate, nucleation and crystal size", J. Appl. Phys. 101 (2007) 053115 1-9.
- P.W. May, Yu. A. Mankelevich, "Experiment and modeling of the deposition of ultrananocrystalline diamond films using hot filament chemical vapor deposition and Ar/CH4/H2 gas mixtures: A generalized mechanism for ultrananocrystalline diamond growth", J. Appl. Phys. 100 (2006) 024301.
- Yu. A. Mankelevich, P. W. May, "New insights into the mechanism of CVD diamond growth: Single Crystal diamond in MW PECVD Reactors" Diamond Relat. Mater. (2008).
- P. W. May, Yu. A. Mankelevich, "From ultrananocrystalline diamond to single crystal diamond growth in hot filament and microwave plasma-enhanced CVD reactors: A unified model for growth rates and grain sizes" J. Phys. Chem. C 112 (2008) 12432–12441. [doi: 10.1021/jp803735a]
- J.E. Butler, Y.A. Mankelevich, A. Cheesman, J. Ma and M.N.R. Ashfold, "Understanding the chemical vapor deposition of diamond: recent progress", J. Phys.: Cond. Matter 21 (2009) 364201 [doi: 10.1088/0953-8984/21/36/364201].
- J.C. Richley, J.N. Harvey, M.N.R. Ashfold, "On the Role of Carbon Radical Insertion Reactions in the Growth of Diamond by Chemical Vapor Deposition Methods", J. Phys. Chem. A 113 (2009) 11416-11422. [doi: 10.1021/jp906065v]
- J.C. Richley, J.N. Harvey and M.N.R. Ashfold, "CH2 group migration between the H-terminated 2×1 reconstructed {100} and {111} surfaces of diamond", in Diamond Electronics and Bioelectronics - Fundamentals to Applications III, edited by P. Bergonzo, J.E. Butler, R.B. Jackman, K.P. Loh, M. Nesladek (Mater. Res. Soc. Symp. Proc. Volume 1203, Warrendale, PA, 2010), paper J17-32. [doi: 10.1557/PROC-1203-J17-32]
- P.W. May and Yu.A. Mankelevich, "Simulations of CVD Diamond Film Growth: 2D Models for the identities and concentrations of gas-phase species adsorbing on the surface", Mater. Res. Soc. Symp. Proc. 1282 (2011) [doi: 10.1557/opl.2011.438].
- J.C. Richley, O.J.L. Fox, M.N.R. Ashfold and Yu.A. Mankelevich, "Combined experimental and modeling studies of microwave activated CH4/H2/Ar plasmas for microcrystalline, nanocrystalline, and ultrananocrystalline diamond deposition", J. Appl. Phys. 109 (2011) 063307. [doi: 10.1063/1.3562185]
- J.C. Richley, J.N. Harvey, and M.N.R. Ashfold, "CH2 Group Migration between H-Terminated 2×1 Reconstructed {100} and {111} Surfaces of Diamond", J. Phys. Chem. C 116 (2012) 7810. [doi: 10.1021/jp300454r]
