 Kinetic Monte Carlo simulations of CVD diamond growth
Kinetic Monte Carlo simulations of CVD diamond growth
Surface processes
Combining a knowledge of the experimental growth conditions and the type of diamond growth that results from these, with measurements of the gas composition in the CVD plasma using diagnostics like REMPI/CRDS and mass spectrometry, has allowed us to develop (in collaboration with Yuri Mankelevich of Moscow State University) a sophisticated model for the reactions and interactions of the various gas-phase species in the plasma. Extrapolating this model to the substrate surface then gives information about the identities, concentrations and energies of all the species striking a growing diamond surface for a given set of deposition conditions (gases, pressure, power, etc.). The next problem is to determine how these species interact with the surface to grow diamond. There are a number of possible processes:
- Adsorption: A gas-phase reactive radical, such as CH3, attaches to a surface radical site.
- Desorption/Etching: An adsorbed CHx species leaves the surface and returns to the gas phase.
- Migration: An adsorbed CHx species migrates around the surface, if there is a neighbouring surface radical site into which it can move.
- Addition: The adsorbing species bonds directly into the diamond lattice (Eley-Rideal-type process), or the migrating species adds onto the lattice (Langmuir-Hinshelwood-type process), either of which propagates the diamond structure.
- β-scission: Any long-chained carbon species CxHy with x>1 adsorbed on the lattice is rapidly etched away.
- Lemming: Species migrating off the top of a step-edge can do so easily, but cannot climb up a step-edge.
The rates for some of these process are known from the literature or previous experiments. Some, however, have to be calculated using ab initio models for surface chemistry.
The kinetic Monte Carlo Model
Our first model 2-dimensional for the (100) surface of diamond was based on a cubic grid, with each square block in the model equivalent to a C atom. An ordered list of the rates for each process and for each species (including new ones that may adsorb on the surface) was created, and a process (adsorption, etching, etc.) for a given species was chosen randomly from this list with a probability proportional to its rate. That process was then performed in the model (e.g. a C is added to the lattice, or removed, or migrates,..) and the rate list recalculated. This sequence was repeated many times and the simulation of the growing diamond surface was then visualised.
The 2D kMC Model
The initial model was only in 2 dimensions, but nevertheless it was able to predict growth rates and basic surface morphologies, and provide an invaluable insight into the growth process.
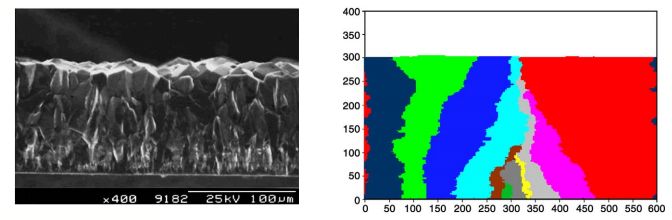
Left: SEM image of a cross-section through a microcrystalline diamond film showing columnar growth.
Right: 2D kMC simulation of the same film using 10 randomly spaced colour-coded seed crystals.
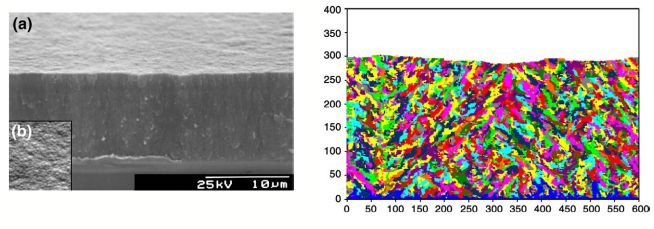
Left: SEM image of a cross-section through an ultra-nanocrystalline diamond film showing a smooth surface and small crystallites, but no columnar growth.
Right: 2D kMC simulation of the same film incorporating renucleation occurring at random times and places, with each new crystallite colour-coded.
The 3D kMC Model
The model was susequently upgraded the model to include the full 3D geometry of the surface, and take into account nearest-neighbour effects upon etching/adsorption of species. This also allowed us to predict growth features like the formation of etchpits and hillocks, and the effect upon growth rate and morphology of defects.
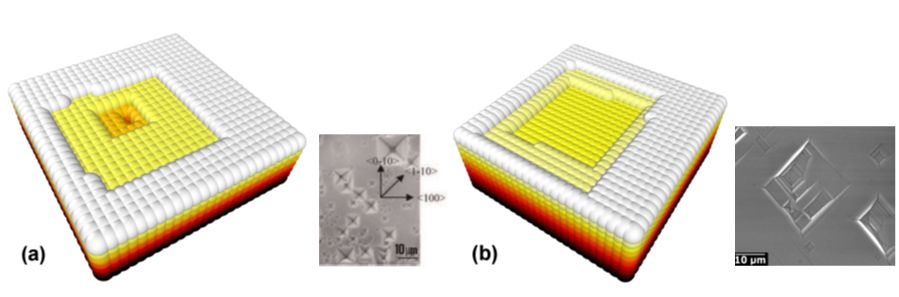
(a) 3D kMC simulation of an inverted pyramid etchpit, similar to those seen when etching single-crystal diamond in oxygen-based gases (as in the SEM).
(b) 3D kMC simulation of a rectangular flat-bottomed etchpit, similar to those seen when etching single-crystal diamond in hydrogen-based gases (as in the SEM).

3D kMC simulation of growth of several layers of diamond under: (a) ultra-nanocrystalline diamond growth, (b) nanocrystalline diamond growth, (c) microcrystalline diamond growth, and (d) single-crystal diamond growth conditions. SCD grows predominantly layer-by-layer due to fast surface migration and step-edge attachment, whereas UNCD grows mainly by direct attachment following adsorption.
The 3D tetrahedral kMC Model
The final version of the growth simulation improved the model for the diamond lattice by using a 3D fully tetrahedral structure with the location of the C atoms being consistent with two interpenetrating fcc lattices, just as in real diamond. The growth model supports adsorption and incorporation of CHx species at monoradical and biradical dimer and trough sites. Once CHx has been incorporated into the lattice as a CH2 bridge, they can be rapidly etched back into the gas phase using a preferential-etching mechanism, or migrate across the surface until they eventually fuse and add to the bulk. The new 3D model has enabled three migration events to be specified and modelled in more detail: adjacent dimer migration, migration into vacant trough sites and migration down atomic steps. Specific dimer-creation and dimer-breaking processes have also now been added to the model. Inclusion of both mechanisms simultaneously increased predicted growth rates and decreased roughness for nanocrystalline and microcrystalline diamond growth conditions. The conclusion is that future kMC models need to specifically include these three migration events as well as models for dimer making and breaking processes, if they are to simulate diamond growth more accurately.
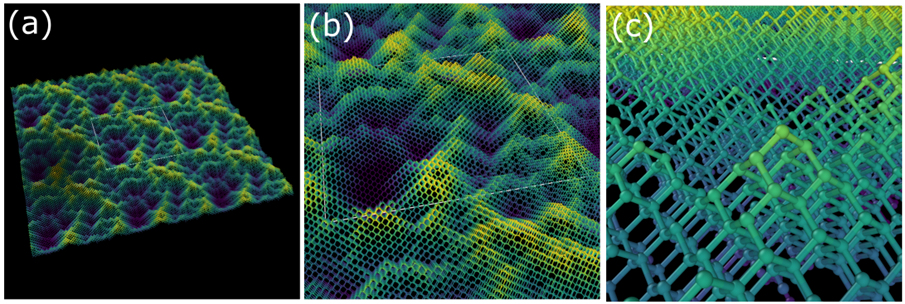
Atomic-level visualisation of thed/ surface, increasing in magnification from (a) to (c). To aid visualisation, the surface is replicated along its periodic boundaries; the original surface dimensions are indicated by a white outline, with false-colouring used to help distinguish the vertical height of atoms and surface features.
References:
- P.W. May, N.L. Allan, M.N.R. Ashfold, J.C. Richley and Yu.A. Mankelevich, "Simplified Monte Carlo Simulations of CVD Diamond Growth", J. Phys.: Cond. Matter 21 (2009) 364203. [doi: 10.1088/0953-8984/21/36/364203]
- P.W. May, J.N. Harvey, N.L. Allan, J.C. Richley and Yu.A. Mankelevich, "Simulations of CVD Diamond Film Growth Using a Simplified Monte Carlo Model", in Diamond Electronics and Bioelectronics — Fundamentals to Applications III, edited by P. Bergonzo, J.E. Butler, R.B. Jackman, K.P. Loh, M. Nesladek (Mater. Res. Soc. Symp. Proc. Volume 1203, Warrendale, PA, 2010), paper J16-02.
- P.W. May, N.L. Allan, M.N.R. Ashfold, J.C. Richley and Yu.A. Mankelevich, "Simulations of Polycrystalline CVD Diamond Film Growth Using a Simplified Monte Carlo Model", Diamond Relat. Mater. 19 (2010) 389-396. [doi: 10.1016/j.diamond.2009.10.030]
- P.W. May, J.N. Harvey, N.L. Allan, J.C. Richley, Yu.A. Mankelevich, "Simulations of CVD Diamond Film Growth Using a Kinetic Monte Carlo Model", J. Appl. Phys 108, (2010) 014905. [doi: 10.1063/1.3437647]
- P. W. May, J. N. Harvey, N. L. Allan, J. C. Richley, Yu. A. Mankelevich, "Simulations of chemical vapor deposition diamond film growth using a kinetic Monte Carlo model and two-dimensional models of Microwave plasma and Hot Filament CVD reactors", J. Appl. Phys. 108 (2010) 114909. [doi: 10.1063/1.3516498]
- W.J. Rodgers, P.W. May , N. L. Allan, J.N. Harvey, "Three-dimensional kinetic Monte Carlo simulations of diamond chemical vapour deposition", 142 J. Chem. Phys. (2015) 214707. [doi: 10.1063/1.4921540]
- M.D.G. Williams, P.W. May, N.L. Allan, "Simulating (100) diamond chemical vapour deposition using a 3D kinetic Monte Carlo code with a tetrahedral model for diamond", in press 2025.
